Đường trung trục d của đoạn thẳng AB chia mặt phẳng thành hai phần I và II như trên hình 10. Cho điểm M thuộc phần I và điểm N thuộc phần II.
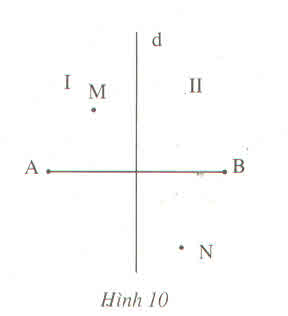
Chứng minh rằng :
a) MA < MB
b) NA > NB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB
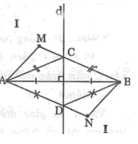
Ta có: NA = ND + DA
Mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có: NB < ND + DB
(bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB.

Nối MA, MB
Gọi C là giao điểm của MB với đường thẳng d, nối CA
Ta có: MB = MC + CB
Mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC, ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB

Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.
Ta có: NA = ND + DA
mà DA = DB (tính chất đường trung trực)
Suy ra: NA = ND + DB (3)
Trong ΔNDB, ta có:
NB < ND + DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA > NB

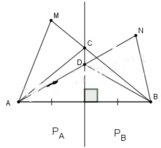
Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.
Ta có: MB = MC + CB
mà CA = CB (tính chất đường trung trực)
Suy ra: MB = MC + CA (1)
Trong ΔMAC ta có:
MA < MC + CA (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra: MA < MB
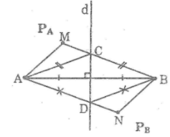

a. Gọi C là giao điểm của MB với đường thẳng d.
Ta có: MB=MC+CB
mà CA=CB(tính chất đường trung trực)
Suy ra: MB=MC+CA(1)
Trong ΔMAC ta có:
MA<MC+CA(bất đẳng thức tam giác)(2)
Từ (1) và (2) suy ra: MA<MB
b.Gọi D là giao điểm của NA với đường thẳng d.
Ta có: NA=ND+DA
mà DA=DB(tính chất đường trung trực)
Suy ra: NA=ND+DB(3)
Trong ΔNDB, ta có:
NB<ND+DB (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: NA>NB
c) Theo phần a và b; với điểm H bất kì ta có:
+ Nếu H nằm trong phần PA thì HA < HB.
+ Nếu H nằm trong phần PB thì HB < HA.
+ Nếu H nằm trên đường thẳng d thì HA = HB (tính chất đường trung trực)
Do đó, để KA < KB thì K nằm trong phần PA.

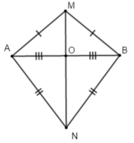
Ta có: MA = MB nên M thuộc đường trung trực của đoạn thẳng AB
Tương tự NA = NB nên N thuộc đường trung trực của đoạn thẳng AB
Suy ra MN là đường trung trực của đoạn thẳng AB
Mà O là trung điểm của AB
Vậy MN vuông góc với AB tại O.
Chọn đáp án C
a: MC+CB=MB
mà CB=CA
nên MC+CA=MB
mà MC+CA<MA
nên MA>MB
b: Gọi D là giao điểm của NA với d
C là giao điểm của CB với d
Ta có:NA=ND+DA
mà DA=DB
nen NA=ND+DB(3)
mà NB<ND+DB
nên NA>NB