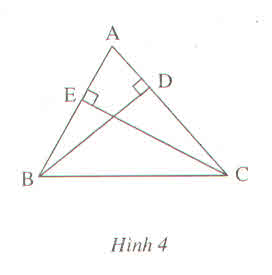
Cho hình 4, chứng minh rằng :
\(BD+CE< AB+AC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2017
3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2
CM
7 tháng 6 2017
Trong ΔABD, ta có ∠(ADB) = 90o
Suy ra: BD < AB (đường vuông góc ngắn hơn đường xiên) (1)
Trong ΔAEC, ta có ∠(AEC) = 90o
Suy ra: CE < AC (cạnh huyền lớn hơn cạnh góc vuông) (2)
Cộng từng vế (1) và (2), ta có: BD + CE < AB + AC.
Xét ΔADB vuông tại D có BD<AB
Xét ΔAEC vuông tại E có CE<AC
Do đó: BD+CE<AB+AC