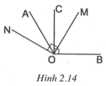
Cho góc AOB ( khác góc bẹt ), tia OM là tia phân giác của góc AOB. Vẽ OA' là tia đối của tia OA, OB' là tia đối của tia OB. ON là tia phân giác của góc A'OB' . Chứng minh góc AOM = góc B'ON
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2020
OA' là tia đối của tia OA, tia OB' là tia đối của tia OB
=> góc AOB = góc A'OB'
mà OM là tịa phân giác góc AOB
=> AOM = góc AOB/ 2
ON là tia phân giác của A'OB'
=> A' A'OB' / 2
mà: góc AOB = góc A'OB'
=> góc AOB /2= góc A'OB'/2
=> góc AOM = góc A'ON
CM
21 tháng 6 2018
a) Tia OM là tia phân giác của góc AOB nên
A
O
M
^
=
B
O
M
^
=
120
°
:
2
=
60
°
.
Ta có O C ⊥ O B ⇒ B O C ^ = 90 ° .
Tia OM nằm giữa hai tia OB, OC nên B O M ^ + C O M ^ = B O C ^
⇒ C O M ^ = 90 ° − 60 ° = 30 °
Tia OC nằm giữa hai tia OA, OB nên A O C ^ + B O C ^ = A O B ^
⇒ A O C ^ = 120 ° − 90 ° = 30 °
Vậy A O C ^ = C O M ^ = 30 ° . (1)
Tia OC nằm giữa hai tia OA, OM nên từ (1) suy ra tia OC là tia phân giác của góc AOM.
b) Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OA nằm giữa hai tia ON, OM nên A O N ^ + A O M ^ = M O N ^ .
Suy ra A O N ^ = M O N ^ − A O M ^ = 90 ° − 60 ° = 30 ° .
Vậy A O N ^ = A O C ^ = 30 ° (2)
Tia OA nằm giữa hai tia ON, OC nên từ (2) suy ra tia OA là tia phân giác của góc CON.