
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\((1)Mg+H_2SO_4\to MgSO_4+H_2\\ (2)MgSO_4+2NaOH\to Mg(OH)_2\downarrow+Na_2SO_4\\ (3)Mg(OH)_2+2HCl\to MgCl_2+2H_2O\\ (4)MgCl_2+2AgNO_3\to Mg(NO_3)_2+2AgCl\downarrow\)
Câu 2:
\(a,Mg,Al,Cu,Ag\\ b,Mg,Al\\ Mg+2HCl\to MgCl_2+H_2\\ 2Al+6HCl\to 2AlCl_3+3H_2\)
\(c,\) Dùng Al vì Al bị thụ động hóa với \(H_2SO_4\) đặc nguội

a: \(Q=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{x-4}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{x-4}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\cdot\left(-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{\sqrt{3}-1+2}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}+1}{\sqrt{3}-4}=\dfrac{-7-5\sqrt{3}}{13}\)
c: Q>1/6
=>Q-1/6>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{1}{6}>0\)
=>\(\dfrac{6\sqrt{x}+12-\sqrt{x}+3}{6\left(\sqrt{x}-3\right)}>0\)
=>\(\dfrac{5\sqrt{x}+9}{6\left(\sqrt{x}-3\right)}>0\)
=>căn x-3>0
=>x>9




19.
\(\left(a+b\right)^2\le2\left(a^2+b^2\right)=4\Rightarrow-2\le a+b\le2\)
\(P=3\left(a+b\right)+ab=3\left(a+b\right)+\dfrac{\left(a+b\right)^2-\left(a^2+b^2\right)}{2}=\dfrac{1}{2}\left(a+b\right)^2+3\left(a+b\right)-1\)
Đặt \(a+b=x\Rightarrow-2\le x\le2\)
\(P=\dfrac{1}{2}x^2+3x-1=\dfrac{1}{2}\left(x+2\right)\left(x+4\right)-5\ge-5\) (đpcm)
Dấu "=" xảy ra khi \(x=-2\) hay \(a=b=-1\)
20.
Đặt \(P=2a+2ab+abc\)
\(P=2a+ab\left(2+c\right)\le2a+\dfrac{a}{4}\left(b+2+c\right)^2=2a+\dfrac{a}{4}\left(7-a\right)^2\)
\(P\le\dfrac{1}{4}\left(a^3-14a^2+57a-72\right)+18=18-\dfrac{1}{4}\left(8-a\right)\left(a-3\right)^2\le18\) (đpcm)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(3;2;0\right)\)

Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)


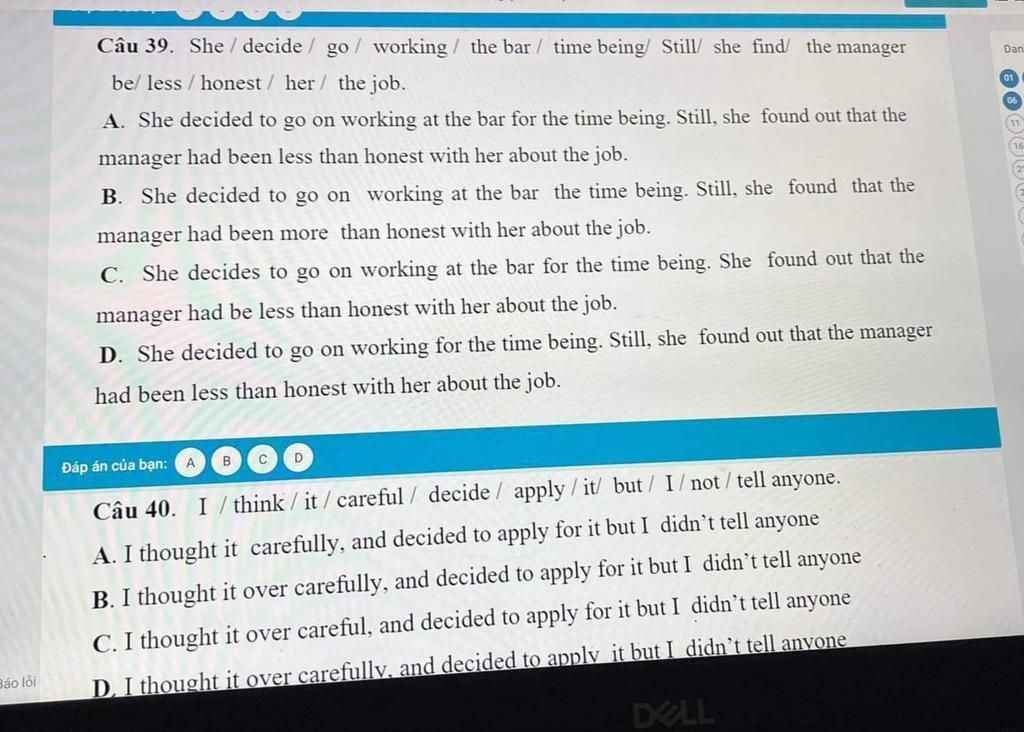

 giúp mik những câu này với ạ
giúp mik những câu này với ạ
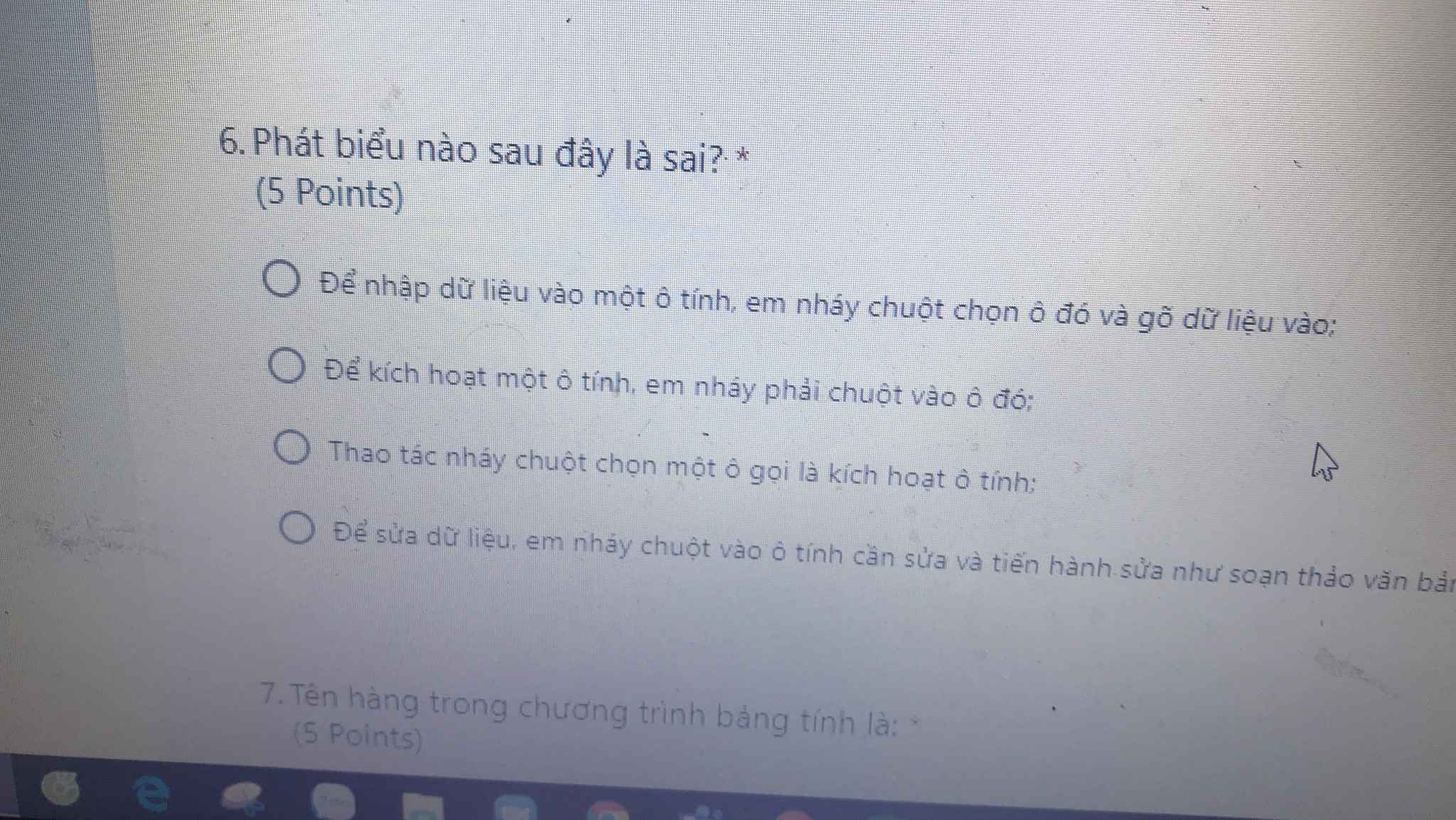
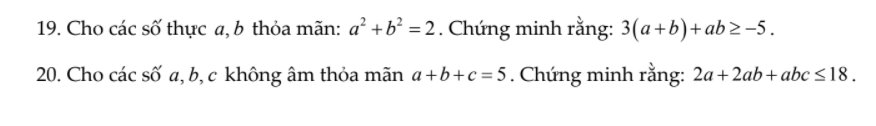

d) \(25x^6-\frac{4y^2}{49}=\left(5x^3\right)^2-\left(\frac{2y}{7}\right)^2=\left(5x^3-\frac{2y}{7}\right)\left(5x^3+\frac{2x}{7}\right)\)
e) \(27x^3-\frac{1}{8}=\left(3x\right)^3-\left(\frac{1}{2}\right)^3=\left(3x-\frac{1}{2}\right)\left(9x^2+\frac{3}{2}x+\frac{1}{4}\right)\)
f ) \(125x^3-1=\left(5x\right)^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
g) \(8x^3+125=\left(2x\right)^3+5^3=\left(2x+5\right)\left(4x^2-10x+25\right)\)
h) \(x^3+\frac{y^3}{8}=x^3+\left(\frac{y}{2}\right)^3=\left(x+\frac{y}{2}\right)\left(x^2-\frac{xy}{2}+\frac{y^2}{4}\right)\)
i ) \(y^3-27x^3=y^3-\left(3x\right)^3=\left(y-3x\right)\left(y^2+3xy+9x^2\right)\)