CMR: \(\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{2013}< \dfrac{1}{4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2021
\(\dfrac{1}{1\cdot2}>\dfrac{1}{2^2}>\dfrac{1}{2\cdot3},\dfrac{1}{2\cdot3}>\dfrac{1}{3^2}>\dfrac{1}{3\cdot4},...,\dfrac{1}{8\cdot9}>\dfrac{1}{9^2}>\dfrac{1}{9\cdot10}\)
\(\Rightarrow\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{8\cdot9}>\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}>\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{9\cdot10}\) \(\Rightarrow1-\dfrac{1}{9}>A>\dfrac{1}{2}-\dfrac{1}{10}\) \(\Rightarrow\dfrac{8}{9}>A>\dfrac{2}{5}\)
15 tháng 3 2018
Ta có :
\(\dfrac{1}{5^2}< \dfrac{1}{4.5}\)
\(\dfrac{1}{6^2}< \dfrac{1}{5.6}\)
....................
\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(\Leftrightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+........+\dfrac{1}{100^2}< \dfrac{1}{4.5}+\dfrac{1}{5.6}+.....+\dfrac{1}{99.100}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+.....+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\left(1\right)\)
Lại có :
\(\dfrac{1}{5^2}>\dfrac{1}{5.6}\)
\(\dfrac{1}{6^2}>\dfrac{1}{6.7}\)
............
\(\dfrac{1}{100^2}>\dfrac{1}{100.101}\)
\(\Leftrightarrow\dfrac{1}{5^2}+\dfrac{1}{6^2}+......+\dfrac{1}{100^2}>\dfrac{1}{5.6}+\dfrac{1}{6.7}+.....+\dfrac{1}{100.101}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+.....+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{5}-\dfrac{1}{101}>\dfrac{1}{6}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
26 tháng 1 2018
Đặt: \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+\dfrac{1}{7^2}+...+\dfrac{1}{100^2}\)
Ta có: \(\left\{{}\begin{matrix}A>\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{100.101}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{5}-\dfrac{1}{101}>\dfrac{1}{6}\\A< \dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{99.100}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{4}-\dfrac{1}{100}< \dfrac{1}{4}\end{matrix}\right.\)
Vậy \(\dfrac{1}{6}< A< \dfrac{1}{4}\)
DL
1
2
8 tháng 5 2022
\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2013^2}\)
Ta có ;
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
...
\(\dfrac{1}{2013^2}< \dfrac{1}{2012.2013}\)
\(\Rightarrow B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2013^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2012.2013}\)
\(\Rightarrow B< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2012}-\dfrac{1}{2013}\)
\(\Leftrightarrow B< 1-\dfrac{1}{2013}\)
\(\Rightarrow B< \dfrac{2012}{2013}\)
Lại có : \(\dfrac{2012}{2013}< \dfrac{3}{4}\)
\(\Rightarrow B< \dfrac{3}{4}\)
* Chắc vậy, sai thì thôg cảm ^^ *
Còn j k hiểu thì ib nha
RP
1
DD
22 tháng 3 2018
a=\(\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot\dfrac{5}{6}\cdot\dfrac{7}{8}\cdot...\cdot\dfrac{79}{80}\)
a<\(\dfrac{2}{3}\cdot\dfrac{4}{5}\cdot\dfrac{6}{7}\cdot\dfrac{8}{9}\cdot...\cdot\dfrac{80}{81}\)
\(\text{a}^2< \dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot\dfrac{4}{5}\cdot\dfrac{5}{6}\cdot\dfrac{6}{7}\cdot\dfrac{7}{8}\cdot\dfrac{8}{9}\cdot...\cdot\dfrac{79}{80}\cdot\dfrac{80}{81}\)
\(\Rightarrow\text{a}^2< \dfrac{1}{81}=\left(\dfrac{1}{9}\right)^2\)
\(\Rightarrow\text{a}< \dfrac{1}{9}\)(dpcm)
Nho tich cho mk nhe
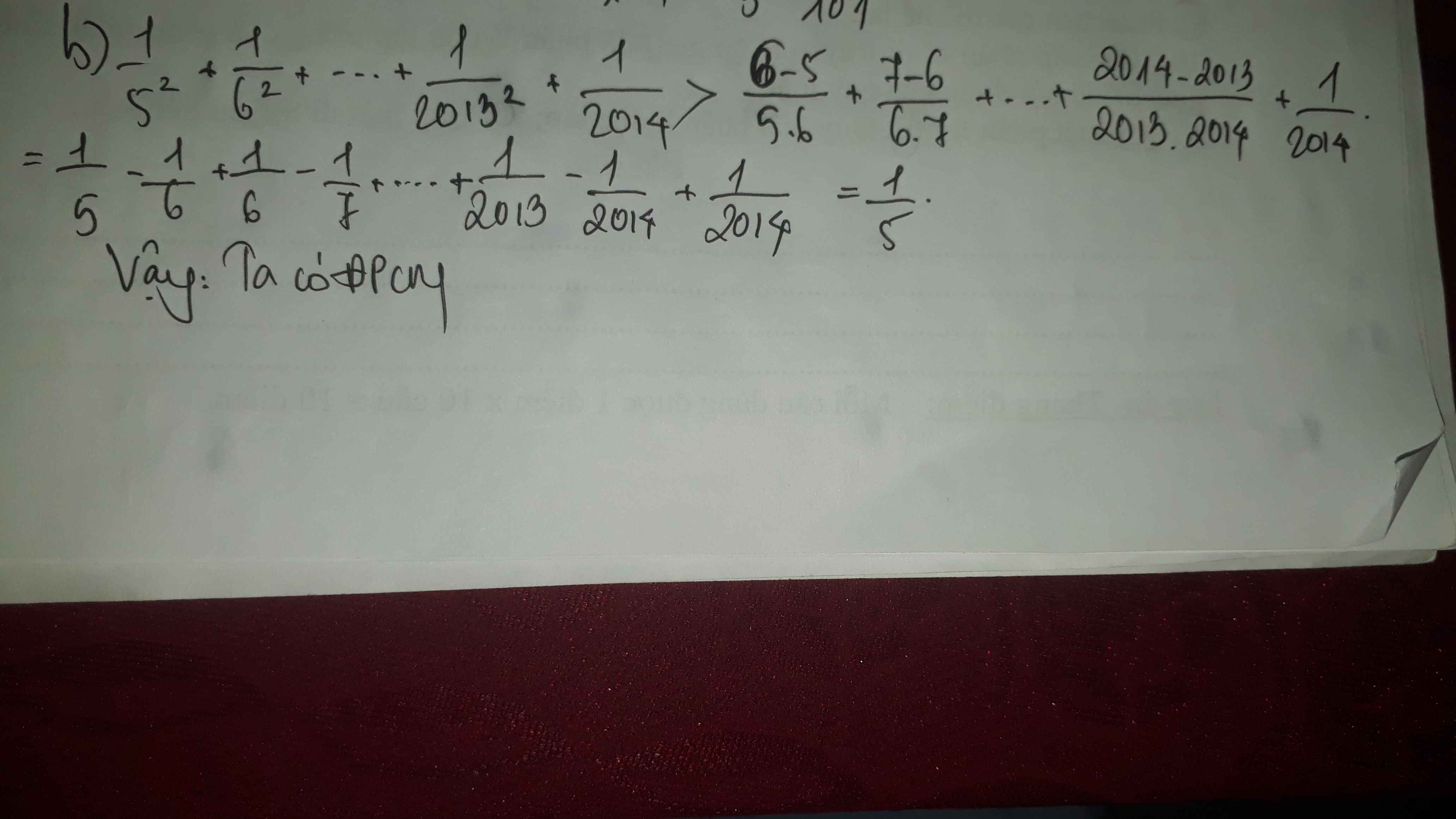
2013 ko mũ 2 nhìn lại đề