Giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: =-3/4+1/2-1/13+3/13=-1/4+2/13=-13/52+8/52=-5/52
b: =10/11+1/11-1/8=1-1/8=7/8
c: =4(2,86+3,14)-30,05+9x0,75
=24-30,05+6,75
=0,7

Theo như lời kể của ông Hiroshi, trong một đêm ông đang tìm kiếm đề tài và nhân vật cho một bộ truyện tranh tâm đắc thì một con mèo hoang nhảy vào nhà, nó kêu vài tiếng rồi nhảy vào lòng ông mà ngủ. Do quá mệt mỏi Hiroshi cũng thiếp đi lúc nào không biết. Sáng hôm sau thức dậy, ông vội vàng bước xuống cầu thang và vấp phải con lật đật của cô con gái, từ đó sinh ra sự kết hợp giữa lật đật và mèo và ra đời nhân vật Doraemon[5].
Theo tập phim 2112: Doraemon ra đời, Doraemon sinh ngày 3 tháng 9 năm 2112 tại Xưởng sản suất Robot ở Tokyo, nhưng trong quá trình chế tạo cậu tình cờ bị trúng phải một tia lửa điện mạnh do bọn cướp bắn ra, khiến cậu bị mất một con ốc vít ở đầu, rơi ra khỏi dây chuyền sản xuất, bị va đập và suýt chút nữa rơi vào lò hỏa thiêu. May mắn Doraemon đã được một cô bạn mèo cứu thoát. Nhưng cũng chính vì bị mất một con ốc nên cậu hay lú lẫn, lấy nhầm bảo bối khiến cho thầy hiệu trưởng trường đào tạo robot nhắc nhở. cậu theo học một lớp học chuyên đào tạo những robot có ích và kết bạn với một nhóm mèo máy có cùng hình dạng (xem Đội quân Doraemon). Vào ngày lễ tốt nghiệp, cậu được gia đình Sewashi nhận về nuôi để trông coi Sewashi. Trước đây, Doraemon có nước da màu vàng và hai tai. Nhưng vào buổi trưa ngày 30 tháng 8 năm 2122, cậu ngủ quên và bị chuột gặm mất đôi tai. Các bác sĩ đã cố gắng sửa chữa tai của Doraemon tại bệnh viện, nhưng do gia đình Sewashi quá nghèo, không đủ tiền để thực hiện việc này nên Doraemon đành phải chấp nhận bỏ đôi tai của mình (còn tập phim nói là do xảy ra sự cố hy hữu trong điều trị), cậu còn bị Noramyako chê cười. Doraemon rất buồn mặc cho Sewashi hết lời an ủi, nước da cậu biến thành màu xanh lam như chúng ta thấy ngày nay. Kể từ hôm đó Doraemon rất sợ và căm ghét bọn chuột tới mức lôi ra những bảo bối hạng nặng ra tiêu diệt chúng như "súng Jumbo" hoặc "Súng tên lửa" trong chương "Chuột và bom", cậu ít tự tin về tình yêu của mình. Doraemon không hiểu tại sao nhà Sewashi lại không thể chữa trị đôi tai cho mình, cậu dùng các bảo bối thời gian quay về quá khứ và gặp Nobita, cụ tổ của Sewashi, và cũng là nguyên nhân gây khó khăn về kinh tế cho con cháu đời sau vì bản chất yếu ớt, hậu đậu. Doraemon quyết định đến giúp Nobita trong cuộc sống, từ đó họ trở thành đôi bạn thân thiết và cùng trải qua bao hiểm nguy, vui có, buồn có. Doraemon bị mất một con vít trong lúc chế tạo do bị bọn cướp bắn trúng, vì vậy mà sau này cậu thường bị hỏng hóc và phải bảo trì thường xuyên. Nhiều lúc trong những tình huống nguy cấp, Doraemon cuống cả lên và lấy ra toàn những thứ linh tinh, chẳng giúp ích được gì.Trong các tập truyện, Doraemon đều được vẽ với hình dáng tròn ủng như trái banh và bàn tay của cậu cũng vậy (Nobita đã lợi dụng điểm yếu này để cậu thường bị thua ở trò oẳn tù tì do chỉ ra được có nắm đấm). Cả người cậu có màu xanh lam, riêng phần trước ngực, nơi đeo túi thần kỳ thì có màu trắng. Ở vài tập truyện đầu tiên, hình dáng Doraemon được vẽ với đầu nhỏ nhưng thân hình lại to. Nhưng sau đó thì Doraemon trở nên cân đối hơn. Doraemon có một cái mồm rộng đến nỗi có thể nuốt vừa một cái chậu lớn. Các số đo thân hình của Doraemon như sau:
- Chiều cao: 129,3 cm
- Cân nặng: 129,3 kg (Nobita cõng Doraemon)
- Nhảy cao: 129,3 cm (khi thấy chuột)
- Công suất tối đa: 129.3 bhp
- Vòng bụng: 129,3 cm
- Đường kính chân: 129,3 mm
- Tốc độ chạy: thông thường: 50 m/s - khi gặp chuột: 129,3 km/h
Như vậy các số đo của Doraemon có một điểm chung: đều là con số 129,3. Ngoài ra, ngày sinh của cậu là 3/9/2112 hay 12/9/3)
Đầu:Đầu Doraemon có cài đặt một máy tính xử lý thông tin thông minh bên trong, làm cho cậu có thể giao tiếp bằng tiếng Nhật và nhận biết được mọi thứ xung quanh y như con người. Nhưng không được nhạy cảm như mong đợi, Doraemon gặp nhiều khó khăn trong việc xử lý các con số, lấy nhầm bảo bối khi cuống lên,... Đầu Doraemon còn cứng như đá, và thật ra cũng là một loại vũ khí rất đắc lực. cậu có thể sử dụng nó để tông vỡ cửa sổ, nổ bình khí gas (Nobita và Vương quốc trên mây), làm kẻ thù bất tỉnh (Nobita và vương quốc robot),...Vì đây là một cậu mèo máy robot của thế kỉ XXII, nên các bộ phận của Doraemon đều có công nghệ cao. Các tính năng ưu việt (nhưng cũng có khi bị hỏng) được kể ra dưới đây:
- Khuôn mặt: Khuôn mặt Doraemon tròn, với chiếc mũi đỏ và 6 sợi ria mép dài bằng nhau. Doraemon rất ghét khi người ta gọi cậu là chồn hay hồ li.
- Mắt: Mắt ngoại tuyến, nhìn ban đêm rõ như ban ngày.
- Mũi:Tròn và màu đỏ như đuôi, siêu thính, độ nhạy gấp 20 lần mũi người (nhưng hiện tại đã bị hư).
- Râu (hay ria mép): 6 sợi râu rađa, có thể nắm bắt được thông tin từ xa, hiện tại đang chờ sửa chữa.
- Miệng: Miệng rộng đến nỗi có thể nuốt cả cái chậu rửa mặt. Răng của Doraemon chỉ được nhìn thấy khi nổi giận (cũng giống với các nhân vật khác).
- Chuông: Được treo trên cổ, có màu vàng, đây là vật đặc trưng của cậu mèo máy, nó cũng được các loại robot khác sử dụng. Khi rung chuông sẽ tạo ra một làn sóng âm thanh đặc biệt và kêu gọi những bạn bè của mèo ú. Nhưng hiện nay cũng đã bị hư, thay vào đó là chiếc chuông camera mini (Nobita và hành tinh muông thú). Trong Nobita và viện bảo tàng bảo bối, Doraemon sẽ ngày càng bị mất hết tư duy và trở thành như một cậu mèo bình thường nếu bị mất chuông.
- Da là một chất đặc biệt chống lại sự ăn mòn kim loại, có độ bền cao, chống bụi. Nhưng nó vô dụng khi gặp thời tiết lạnh hay nóng quá. Bên trong là lò nguyên tử, tạo ra năng lượng cho mèo ú. Trong tập phim 2112: Doraemon ra đời, da vốn là màu xanh lam, còn màu vàng chỉ là nước sơn và chuyển sang màu xanh khi cậu khóc quá nhiều. Ngoài ra, da ở phần chân có thiết bị phản trọng lực, vì vậy chân Doraemon luôn cách mặt đất 3 mm (cũng là lý do mà cậu chả bao giờ đi giày).
- Tay: Hình tròn trắng và không có vân tay. Doraemon thường bị thua trong những cuộc thi "oẳn tù tì" do chỉ ra được nấm đấm, và Nobita đã biết lợi dung điều bất tiện này (ra kéo hoặc bao,...). Nhưng có lực hút và cầm được mọi vật không cần ngón.
- Túi thần kỳ: Sử dụng công nghệ không gian 4 chiều, một kho chứa vô tận. Doraemon thường đeo nó ở trước bụng và cất giữ bảo bối, cậu có một chiếc tương tự gọi là túi sơ-cua để dưới gối, dùng khi quên mang theo và thông hai đầu với nhau. Ngoài ra nó còn được dùng để chứa các thứ linh tinh khác như bánh rán, chén đũa,...
- Chân: Chân dẹt màu trắng, có thể bước đi nhẹ nhàng không gây tiếng động.
- Đuôi: Hình tròn màu đỏ, đây là công tắc toàn bộ hệ thống của Doraemon, nếu kéo nó Doraemon sẽ rơi vào trạng thái bất động, được sử dụng để tiết kiệm năng lượng. Nhưng trong bộ truyện màu phát hành năm 1970, khi kéo cái đuôi, Doraemon lại tàng hình.
Doraemon là robot mèo máy cũ xảy ra sự cố, đó là lý do khiến các bộ phận như "chuông gọi mèo" và "Râu ra-đa" hỏng liên tục, ngoài "thiết bị cảm nhận âm thanh từ xa". Vì vậy, thi thoảng cậu cũng tự trang bị cho mình những linh kiện mới rẻ tiền. Như trong tập truyện dài Doraemon: Nobita và hành tinh muông thú, cậu thay chuông gọi mèo thành máy chụp hình mini treo cổ, dù các bộ phận khác vẫn bị bỏ rơi và chưa được đem đi sửa. Thực tế hơn, thế giới tương lai của Doraemon quy định mỗi năm phải đi kiểm tra sức khỏe toàn diện định kỳ một lần (Doraemon bị ốm?, tập 45). Khi đó, những bộ phận hỏng hóc sẽ được sửa chữa. Nhưng những thiết bị hỏng hóc trên người Doraemon cứ như vậy mãi do cậu không chịu đi kiểm tra, sợ khám sức khỏe vì cho rằng nếu vậy thì Nobita sẽ không thể sống tốt như trước.
Doraemon là một cậu mèo máy vui tính, khá nhanh trí nhưng đôi lúc lại lẩm cẩm. Cậu ta mắc chứng ám ảnh sợ chuột (musophobia), đặc biệt là chuột nhắt. Đó là do khi ở thế kỉ XXII, khi ngủ quên, cậu đã bị một con chuột gặm cụt mất đôi tai. Mỗi khi gặp chuột nhắt, cậu đều chạy trốn với tốc độ rất nhanh (129,3 km/giờ), nhiều khi sợ quá và bất tỉnh. Đặc điểm này của Doraemon đã gây ra nhiều điều rắc rối cho mọi người và Nobita cũng lợi dụng điều này để vòi vĩnh những bảo bối trong chiếc túi thần kỳ. Hàng ngày, Doraemon phải chăm sóc suốt ngày suốt đêm cho Nobita, không rời khỏi nhà dù là ai đó rủ cậu đi chơi, đến khi nào Nobita đi đâu đó không có ở nhà thì cậu mới được tự do, trong thời gian đó thì Mèo Ú sẽ tận dụng thời gian đi mua bánh rán hay đi trò chuyện với các cậu mèo hàng xóm và cậu cũng chăm sóc mấy bạn mèo hàng xóm, người làm cậu tốn công nhất là Nobita. Tuy tên của Doraemon không xuất phát từ bánh dorayaki nhưng loạt truyện đã dựa trên sự giống nhau phát âm (dora-), thứ bánh này (các bản dịch tiếng Việt gọi là bánh rán) đã trở thành thức ăn mà Doraemon thích nhất. Bánh rán mà Doraemon thích là từ khi cô bạn gái Noramyako của cậu cho cậu ăn để an ủi, động viên, xua tan chuyện buồn điểm kém thời thế kỷ 22 Doraemon ra đời. Đây là thứ bánh truyền thống của Nhật Bản. Doraemon từng nói rằng nếu không được ăn bánh rán quá 3 ngày thì cậu sẽ không sống nổi, thường hay bức rứt không yên. Chính vì thích bánh rán nên cậu thường được mời ăn để thuyết phục cậu mượn bảo bối nhất là Nobita. Trong các tập truyện tranh Doraemon, ban đầu cậu thường từ chối Nobita khi cậu mượn bảo bối. Nhưng sau đó cậu đều đồng tình và cho mượn. Có điều là các bảo bối đều được Nobita sử dụng không đúng mục đích và thường có những cảnh như khoe Shizuka hay bị Jaian, Suneo tịch thu, sau đó gây ra các tình huống trớ trêu khiến cho truyện Doraemon trở nên hấp dẫn.Trong những cuộc phiêu lưu,Doraemon luôn là vị cứu tinh của chúng bạn nhờ chiếc túi thần kì chứa đủ các bảo bối của thế kỉ 22 nhưng hơn cả đó là cậu có một tấm lòng nhân hậu,dũng cảm,luôn giúp đỡ bạn bè khi khó khăn. Vì là một Robot cao cấp của tương lai, nên Doraemon vẫn bị muỗi đốt, bỏng, cảm lạnh, buồn ngủ, đổ mồ hôi như con người thật để tiện chăm sóc và sống cùng trẻ nhỏ, Doraemon rất ghét mùa đông vì sợ lạnh và không thể chịu nổi thời tiết lạnh giá, hay cuộn tròn bên bàn sưởi, ôm lò sưởi và đắp chăn kín người.
Doraemon còn có một cô bạn gái (mèo thật) là Tama hay Mimi, cậu đã từng vất vả để chinh phục cô nàng đỏng đảnh này. Bên cạnh đó cậu cũng làm quen với nhiều mèo khác và có cả nhóm mèo bạn thân của Doraemon. Thỉnh thoảng ta thấy cô và Doraemon cùng đi picnic (các tập truyện ngắn), Nobita rất bực mình vì đôi khi Doraemon đi chơi với Mimi mà không cho cậu mượn bảo bối. Ở thế kỷ 22, Doraemon cũng có một cô em gái là Dorami. Cậu ta từng có một cô bạn gái là mèo máy tên là Noramyako (ノラミャー子) những đã chia tay vì cô cảm thấy Doraemon quá lùn so với cô và một lý do khác nữa là do khi Doraemon mất tai phải băng bó nên bị Noramyako chế nhạo. Doraemon cũng xuất hiện trong truyện Đội quân Doraemon với vai trò là một trong bảy thành viên của đội quân cùng tên. Trong truyện Doraemon bóng chày với số áo 10 ở vị trí giao bóng nhưng ném bóng khá tệ. Cuộc sống thực sự của Doraemon thường không được phản ánh đầy đủ mà chủ yếu là qua những tình huống liên quan đến Nobita. Những món bảo bối mà Doraemon mua được xuất phát từ việc bán tiền cổ mà hàng tháng mẹ Nobita cho (500 yên/tháng) với giá cao để lấy tiền hơn 100 năm sau mà thời Sewashi sử dụng nên mọi bảo bối trong tay Doraemon đều được mua từ cửa hàng bách hóa tương lai.
Doraemon là nhân vật hoạt hình duy nhất trong số 22 nhân vật nổi bật của châu Á (Asian Heroes) trong một bài báo có tựa đề The Cuddliest Hero in Asia(Anh hùng đáng yêu nhất ở châu Á) do tạp chí TIME bầu chọn[6]. Tháng 3 năm 2008, chính phủ Nhật Bản đã chọn Doraemon là Đại sứ hoạt hình chính thức của Nhật Bản trong một buổi lễ do đích thân Ngoại trưởng Nhật Bản Komura Masahiko chủ trì.[7]. Với những bảo bối của mình, Doraemon theo một cuộc bầu chọn năm 2007 trên trang tin tức Oricon thậm chí đã được xếp thứ hai trong "danh sách các nhân vật manga quyền năng nhất", chỉ sau Son Goku của Bảy viên ngọc rồng[8]. Một cuộc thăm dò khác cũng được Oricon công bố ngày 14 tháng 4 năm 2008 với đối tượng là những người hâm mộ hoạt hình Nhật Bản theo câu hỏi Bạn muốn trở thành nhân vật anime nào nhất?, trong đó nhân vật Doraemon đứng ở vị trí thứ hai, sau Son Goku (Bảy viên ngọc rồng).[9]Doraemon còn xuất hiện trong nhiều lĩnh vực khác nhau. Hãng ESP Guitars đã chế tạo một loại guitar mang hình dáng Doraemon [10]. cậu mèo máy cùng các nhân vật vật khác trong tác phẩm cùng tên cũng xuất hiện trong video âm nhạc cho đĩa đơn "From a Distance", trích từ album Bicycles & Tricycles của The Orb. Hơn 50 trò chơi video-chỉ tiếng Nhật, bắt đầu từ hệ máy Arcadia 2001 của hãng Emerson lấy Doraemon làm nhân vật chính. cậu mèo máy còn có thể thấy trong loạt trò chơi Taiko no Tatsujin (chỉ từ 11 - 13), Meccha! Taiko no Tatsujin DS: 7tsu no Shima no Daibouken, và Taiko no Tatsujin Wii. Kể từ năm 2000, công ty Bunmeido đã bán những phiên bản giới hạn những chiếc bánh dorayaki với tên gọi Doraemon Dorayaki mỗi năm vào khoảng tháng 3 (tháng trình chiếu các bộ phim dài) và tháng 9 (tháng sinh nhật của Doraemon). Ngày 3 tháng 9 năm 2009, biểu trưng của Google tiếng Nhật đã thay đổi với hình ảnh của Doraemon và những bảo bối quen thuộc như trực thăng tre, cánh cửa thần kì, đèn pin thu nhỏ để kỷ niệm sinh nhật cậu mèo máy[11]. Ở phạm vi ngoài Nhật Bản, nhân vật Broadband của Ủy ban Truyền thông Liên bang có nhiều nét giống Doraemon, việc này đã gây ra những tranh cãi về vấn đề bản quyền giữa Shogakukan với Ủy ban này[12]. Hình ảnh Doraemon cũng là ý tưởng ra đời các tác phẩm Đội quân Doraemon và Doraemon bóng chày.
k nha

Hai câu thơ cuối của bài thơ là cái tình say đắm của tác giả trước vẻ đẹp của thiên nhiên. ... Hai câu cuối của bài thơ Cảnh khuya đã bộc lộ vẻ đẹp và chiều sâu tâm hồn của tác giả vị lãnh tụ cách mạng vĩ đại của dân tộc.

con co ti thoi gian giup minh voi co giao cho lam de thi thu kho qua giup minh voi nhanh len .de thi thu kho qua

T có dãy số tự nhiên lẻ liên tiếp thì các số hạng liên tiếp hơn kém nhau 2 đơn vị.
Số số hạng = (Số cuối - số đầu) : Khoảng cách + 1
Tổng = (Số cuối + số đầu) x Số số hạng : 2
Tổng 10 số trên là: 67 x 10 = 6 700
Tổng của số đầu và số cuối là: 6 700 x 2 : 10 = 1 340
Hiệu của số đầu và số cuối là: (10 - 1) x 2 = 18
Vậy số cuối là : (1 340 + 18) : 2 = 679
Số đầu là: 679 - 18 = 661

cái này bạn phải nhờ thợ sửa máy tính chứ mk cung học máy tính này
Bạn bật unikey sau đó nhấn mặc định và nhấn đóng nhé
kb và vô team mik

Tuy giàu nhưng cô ấy ăn uống rất đơn giản, không cần nem công chả phương
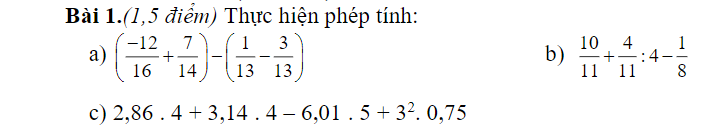
 giup minh bai nay voi .....minh ci biet dia li voi toan thoi
giup minh bai nay voi .....minh ci biet dia li voi toan thoi
\(1,\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8+6\sqrt{x-1}}=5\)
\(ĐKXĐ:x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1+6\sqrt{x-1}+9}=5\)
\(\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(\sqrt{x-1}+3\right)^2}=5\)
\(\left|\sqrt{x-1}-2\right|+\left|\sqrt{x-1}+3\right|=5\)
\(\orbr{\begin{cases}2-\sqrt{x-1}+\sqrt{x-1}+3=5\\\sqrt{x-1}-2+\sqrt{x-1}+3=5\end{cases}\orbr{\begin{cases}5=5\left(TM\forall x\right)\\\sqrt{x-1}=2\end{cases}\orbr{\begin{cases}5=5\\x=5\left(TM\right)\end{cases}}}}\)
vậy pt có nghiệm là \(1\le x\le+\infty\)
\(2,\sqrt{x+\sqrt{6x-9}}+\sqrt{x-\sqrt{6x-9}}=\sqrt{6}\)
\(ĐKXĐ:x\ge\frac{3}{2}\)
\(\sqrt{x+\sqrt{6}\sqrt{x-\frac{3}{2}}}+\sqrt{x-\sqrt{6}\sqrt{x-\frac{3}{2}}}=\sqrt{6}\)
\(\sqrt{x-\frac{3}{2}+\sqrt{6}\sqrt{x-\frac{3}{2}}+\frac{3}{2}}+\sqrt{x-\frac{3}{2}-\sqrt{6}\sqrt{x-\frac{3}{2}}+\frac{3}{2}}=\sqrt{6}\)
\(\sqrt{\left(\sqrt{x-\frac{3}{2}}+\frac{3}{2}\right)^2}+\sqrt{\left(\sqrt{x-\frac{3}{2}}-\frac{3}{2}\right)^2}=\sqrt{6}\)
\(\left|\sqrt{x-\frac{3}{2}}+\frac{3}{2}\right|+\left|\sqrt{x-\frac{3}{2}}-\frac{3}{2}\right|=\sqrt{6}\)
\(\orbr{\begin{cases}\sqrt{x-\frac{3}{2}}+\frac{3}{2}+\frac{3}{2}-\sqrt{x-\frac{3}{2}}=\sqrt{6}\\\sqrt{x-\frac{3}{2}}+\frac{3}{2}-\frac{3}{2}+\sqrt{x-\frac{3}{2}}=\sqrt{6}\end{cases}}\orbr{\begin{cases}3=\sqrt{6}\\2\sqrt{x-\frac{3}{2}}=\sqrt{6}\end{cases}}\)
\(\orbr{\begin{cases}3=\sqrt{6}\left(KTM\right)\\x=3\left(TM\right)\end{cases}}\)
\(3,\sqrt{x^2-5x+6}+\sqrt{x+1}=\sqrt{x-2}+\sqrt{x^2-2x-3}\)
\(ĐKXĐ:x\ge3\)
\(\left(\sqrt{x^2-5x+6}-\sqrt{2}\right)+\left(\sqrt{x+1}-\sqrt{5}\right)=\left(\sqrt{x-2}-\sqrt{2}\right)+\left(\sqrt{x^2-2x-3}-\sqrt{5}\right)\)
\(\frac{x^2-5x+4}{\sqrt{x^2-5x+6}+\sqrt{2}}+\frac{x-4}{\sqrt{x+1}+\sqrt{5}}=\frac{x-4}{\sqrt{x-2}+\sqrt{2}}+\frac{x^2-2x-8}{\sqrt{x^2-2x-3}+\sqrt{5}}\)
\(\frac{\left(x-4\right)\left(x-1\right)}{\sqrt{x^2-5x+6}+\sqrt{2}}+\frac{x-4}{\sqrt{x+1}+\sqrt{5}}=\frac{x-4}{\sqrt{x-2}+\sqrt{2}}+\frac{\left(x-4\right)\left(x+2\right)}{\sqrt{x^2-2x-3}+\sqrt{5}}\)
\(\left(x-4\right)\left(\frac{x-1}{\sqrt{x^2-5x+6}+\sqrt{2}}+\frac{1}{\sqrt{x+1}+\sqrt{5}}-\frac{1}{\sqrt{x-2}+\sqrt{2}}-\frac{x+2}{\sqrt{x^2-2x-3}+\sqrt{5}}\right)=0\)
\(\orbr{\begin{cases}x=4\left(TM\right)\\\frac{x-1}{\sqrt{x^2-5x+6}+\sqrt{2}}+\frac{1}{\sqrt{x+1}+\sqrt{5}}-\frac{1}{\sqrt{x-2}+\sqrt{2}}-\frac{x+2}{\sqrt{x^2-2x-3}-\sqrt{5}}=0\end{cases}}\)
bạn lập luận cái dưới vô nghiệm
10, \(đk:x\ge\frac{1}{2}\)
\(\sqrt{x+3}+\sqrt{2x-1}=3\)
\(\Leftrightarrow\sqrt{x+3}+\sqrt{2x-1}-3=0\)
\(\Leftrightarrow\frac{\left(\sqrt{x+3}-2\right)\left(\sqrt{x+3}+2\right)}{\sqrt{x+3}+2}+\frac{\left(\sqrt{2x-1}-1\right)\left(\sqrt{2x-1}+1\right)}{\sqrt{2x-1}+1}=0\)
\(\Leftrightarrow\frac{x+3-4}{\sqrt{x+3}+2}+\frac{2x-1-1}{\sqrt{2x-1}+1}=0\)
\(\Leftrightarrow\frac{x-1}{\sqrt{x+3}+2}+\frac{2x-2}{\sqrt{2x-1}+1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(\frac{1}{\sqrt{x+3}+2}+\frac{2}{\sqrt{2x-1}+1}\right)=0\)
với x >= 1/2 thì ngoặc thứ 2 > 0
\(\Leftrightarrow x=1\left(tm\right)\)
8, đk \(\orbr{\begin{cases}x\ge0\\x\le-8\end{cases}}\)
\(x^2+8x-3=2\sqrt{x\left(x+8\right)}\)
\(\Leftrightarrow x\left(x+8\right)-3=2\sqrt{x\left(x+8\right)}\)
đặt \(\sqrt{x\left(x+8\right)}=a\left(a\ge0\right)\)
pt trở thành : \(a^2-3=2a\Leftrightarrow a^2-2a-3=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=3\left(tm\right)\\a=-1\left(loai\right)\end{cases}}\)
a = 3 => \(\sqrt{x\left(x+8\right)}=3\Leftrightarrow x^2+8x-9=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\left(tm\right)\\x=-9\left(tm\right)\end{cases}}\)
7, đk \(x>0\)
\(\sqrt{\frac{x^2+x+1}{x}}+\sqrt{\frac{x}{x^2+x+1}}=\frac{7}{4}\)
\(\Leftrightarrow\frac{x^2+x+1}{x}+\frac{x}{x^2+x+1}+2\sqrt{\frac{x^2+x+1}{x}\cdot\frac{x}{x^2+x+1}}=\frac{49}{16}\)
\(\Leftrightarrow\frac{x^4+x^2+1+2x^3+2x^2+2x+x^2}{x\left(x^2+x+1\right)}+2=\frac{49}{16}\)
\(\Leftrightarrow\frac{x^4+2x^3+4x^2+2x+1}{x\left(x^2+x+1\right)}=\frac{17}{16}\)
\(\Leftrightarrow16x^4+32x^3+64x^2+32x+16=17x^3+17x^2+17x\)
\(\Leftrightarrow16x^4+15x^3+47x^2+15x+16=0\)
bấm mt nó ra nghiệm ảo :v