tìm m để hàm số y= | x^3 - 3x^2 +mx -1 | có 5 điểm cực trị
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

bước 1: ta tính y'
bước 2: giải pt y'=0 tìm ra xi
bước 3 tính y''
để hàm số có cực đại thì y''(xi)<0
đểhàm số có cực tiểu thì y''(xi)>0
giả các pt ta tìm đc điều kiện của m hàm số có cực đại, cực tiểu

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 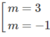
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.



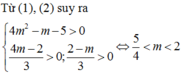
Đặt \(x^3-3x^2+mx-1=f\left(x\right)\).
Để \(\left|f\left(x\right)\right|\)có \(5\)điểm cực trị thì phương trình \(f\left(x\right)=0\)có ba nghiệm phân biệt.
\(x^3-3x^2+mx-1=0\)
\(\Leftrightarrow m=\frac{-x^3+3x^2+1}{x}=g\left(x\right)\)(vì \(x=0\)không là nghiệm của phương trình)
\(g'\left(x\right)=-\frac{2x^3-3x^2+1}{x^2}\)
\(g'\left(x\right)=0\Rightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=1\end{cases}}\)(có \(x=1\)là nghiệm kép)
\(g'\left(x\right)\)không xác định khi \(x=0\).
BBT (bạn tự vẽ).
Từ BBT ta thấy \(g\left(x\right)=m\)có ba nghiệm phân biệt khi \(m< \frac{-15}{4}\).
Vậy \(m< -\frac{15}{4}\).