Cho hàm số f(x) = 2x\(^2\)-x. Giải phương trình f '(x)\(\sqrt{x^2+1}\) = 2x\(^2\)+2x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
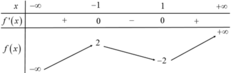
Đồ thị hàm số y = f ( x ) = x 3 - 3 x + 1 có dạng:
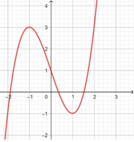
Dựa vào đồ thị ta thấy phương trình f(x) =0 có 3 nghiệm


![]()
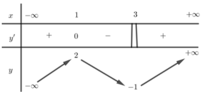
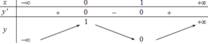
Quan sát bảng biến thiên ta thấy phương trình này có 2 nghiệm.
Chọn D

Đáp án A
Ta có
![]()
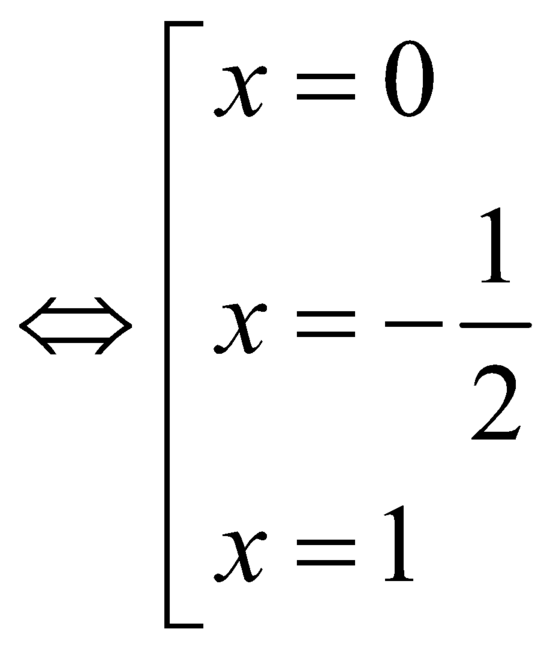 .
.
Bảng xét dấu:
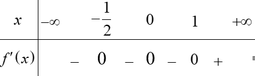
Suy ra hàm số có một điểm cực trị.

\(x>1\)
\(f'\left(x\right)=\left(2x+2\right)\sqrt{x-1}+\frac{x^2+2x}{2\sqrt{x-1}}=\frac{5x^2+2x-4}{2\sqrt{x-1}}\)
\(f'\left(x\right)\ge0\Leftrightarrow\frac{5x^2+2x-4}{\sqrt{x-1}}\ge0\Leftrightarrow5x^2+2x-4\ge0\)
\(\Rightarrow x>1\)

Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x
Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x


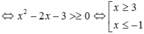
Ta có:f'(x)=4x-1
=>f'(x)\(\sqrt{x^2+1}=2x^2+2x+1\)
<=>(4x-1)\(\sqrt{x^2+1}=2x^2+2x+1\)
Nhận xét: vế phải > 0 nên đk để phương trình có nghiệm:x>\(\dfrac{1}{4}\)
Từ điều kiện trên phương trình
<=>(16x2-8x+1)(x2+1)=4x4+8x3+8x2+4x+1
<=>16x4+16x2-8x3-8x+x2+1=4x4+8x3+8x2+4x+1
<=>12x4-16x3+9x2-12x=0
<=>x(12x3-16x2+9x-12)=0
<=>x(3x-4)(4x2+3)=0
<=>x=0 hoặc x=\(\dfrac{4}{3}\)(do 4x2+3>0)
Vậy...
x=0 loại