OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NL
Nhi Le
12 tháng 5 2019

Cho hàm số f(x)=(x\(^2\)+2*x)*\(\sqrt{x-1}\) .Giải bất phương trình f ' (x) >=0

M.n giải hộ mình câu này với ạ.Cảm ơn mn nhiều

#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2019

\(x>1\)

\(f'\left(x\right)=\left(2x+2\right)\sqrt{x-1}+\frac{x^2+2x}{2\sqrt{x-1}}=\frac{5x^2+2x-4}{2\sqrt{x-1}}\)

\(f'\left(x\right)\ge0\Leftrightarrow\frac{5x^2+2x-4}{\sqrt{x-1}}\ge0\Leftrightarrow5x^2+2x-4\ge0\)

\(\Rightarrow x>1\)

Đúng(0)
NL
Nhi Le
13 tháng 5 2019

Mình k hiểu bước đầu lắm.Bạn giải thích hộ mình với

Đúng(0)
NL
Nhi Le
12 tháng 5 2019

Cho hàm số y=f(x)=x^4-2*x^2-4có đồ thị (C).Tìm toạ độ những điểm trên đồ thị (C) sao cho tiếp tuyến của đồ thị tại các điểm đó song song với trục hoành.

M.n giải hộ mình,mình cần gấp ạ.Cảm ơn mn nhiều!

#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2019

Tiếp tuyến song song trục hoành \(\Rightarrow\) hệ số góc của tiếp tuyến bằng 0 \(\Rightarrow\) đó là tiếp tuyến tại các cực trị

\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-4\\x=-1\Rightarrow y=-5\\x=1\Rightarrow y=-5\end{matrix}\right.\)

Vậy các điểm đó là \(A\left(0;-4\right);B\left(-1;-5\right);C\left(-1;-5\right)\) (1 chú ý nhỏ là tiếp tuyến tại B và C trùng nhau)

Đúng(0)
RY
rim ye
6 tháng 5 2017

Cho hàm số f(x) = 2x\(^2\)-x. Giải phương trình f '(x)\(\sqrt{x^2+1}\) = 2x\(^2\)+2x+1
#Toán lớp 11
1
XT
Xuân Tuấn Trịnh
6 tháng 5 2017

Ta có:f'(x)=4x-1

=>f'(x)\(\sqrt{x^2+1}=2x^2+2x+1\)

<=>(4x-1)\(\sqrt{x^2+1}=2x^2+2x+1\)

Nhận xét: vế phải > 0 nên đk để phương trình có nghiệm:x>\(\dfrac{1}{4}\)

Từ điều kiện trên phương trình

<=>(16x2-8x+1)(x2+1)=4x4+8x3+8x2+4x+1

<=>16x4+16x2-8x3-8x+x2+1=4x4+8x3+8x2+4x+1

<=>12x4-16x3+9x2-12x=0

<=>x(12x3-16x2+9x-12)=0

<=>x(3x-4)(4x2+3)=0

<=>x=0 hoặc x=\(\dfrac{4}{3}\)(do 4x2+3>0)

Vậy...

Đúng(0)
N
ngonhuminh
8 tháng 7 2017

x=0 loại

Đúng(0)
LT
Lê Thanh Phú
14 tháng 4 2019

Giải các phương trình sau:
1. F'(x)=0 với y(x)=3x+60/x -64/x^3+5
2. F'(x)=0 với f(x)=1-sin(pi+x)+2cos((3pi+x)/2)
3. F'(x)=0 với f(x)=sin3x/3 +cosx -√3*(sinx+(cos3x/3))
4. G'(x)=0 với g(x)=sin3x -√3*cos3x +3*(cosx -√3*sinx)
#Toán lớp 11
0
KJ
kwon ji yong
10 tháng 4 2017

CÂU HỎI: Cho hàm số y = f(x) = x3 -3x. Viết phương trình tiếp tuyến:

a) Tại điểm có tung độ bằng 2.

b) Biết tiếp tuyến đi qua M(-1;2).

c) Biết hệ số góc của tiếp tuyến = -3.

( Mọi người giải chi tiết dùm mình với. Cám ơn!)
#Toán lớp 11
1
CT
chu thị ánh nguyệt
11 tháng 4 2017

x3 vs 3x...???

Đúng(0)
AT
Anh Trịnh
11 tháng 12 2019

Giải phương trình

(2sinx + 1) (\(\sqrt{3}\sin x\) + \(2\cos^2x\) - 1) = Sin2x + cosx

làm giúp mình với huhu
#Toán lớp 11
1
LM
lê minh châu
14 tháng 12 2019

\(\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1\right)-\sin2x-\cos x=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1-2\cos^2x+1-\cos x\right)=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x-\cos x\right)=0\Rightarrow\left[{}\begin{matrix}2\sin x+1=0\\\sqrt{3}\sin x-\cos x=0\end{matrix}\right.\)

Đúng(0)
L
LVTA
15 tháng 4 2021

cho hàm số : f(x)=∛x . tính f ' (8)
#Toán lớp 11
1
H
HT2k02
15 tháng 4 2021

\(f'\left(x\right)=\left(\sqrt[3]{x}\right)'=\dfrac{1}{3\sqrt[3]{x^2}}\\ f'\left(8\right)=\dfrac{1}{3\sqrt[3]{8^2}}=\dfrac{1}{12}\)

Đúng(1)
NL
Nhi Le
15 tháng 5 2019
C1/Chứng minh rằng phương trình \(x^3+mx^2+\left(m-3\right)x-1=0\)(m là tham số),có 3 nghiệm phân biệt với mọi m. C2/Cho f(x)=\(\frac{x^3}{3}\)+(m-1)\(x^2\)+(m+1)\(x\).Tìm giá trị của m để f ' (x)\(\ge0\) với mọi m. C3/Phương trình \(2x^3+3x^2+mx-2=0\)có ít nhất 1 nghiệm trong khoảng (-1;1) khi m? ...
Đọc tiếp

C1/Chứng minh rằng phương trình \(x^3+mx^2+\left(m-3\right)x-1=0\)(m là tham số),có 3 nghiệm phân biệt với mọi m.

C2/Cho f(x)=\(\frac{x^3}{3}\)+(m-1)\(x^2\)+(m+1)\(x\).Tìm giá trị của m để f ' (x)\(\ge0\) với mọi m.

C3/Phương trình \(2x^3+3x^2+mx-2=0\)có ít nhất 1 nghiệm trong khoảng (-1;1) khi m?
#Toán lớp 11
2
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 5 2019

Câu 1:

Đặt \(f\left(x\right)=x^3+mx^2+\left(m-3\right)x-1\)

Ta có \(f\left(0\right)=-1\) ; \(f\left(-1\right)=1\)

\(\Rightarrow f\left(0\right).f\left(-1\right)< 0\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)

Mặt khác \(\left\{{}\begin{matrix}f\left(0\right)=-1< 0\\\lim\limits_{x\rightarrow+\infty}=+\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)

\(\left\{{}\begin{matrix}f\left(-1\right)=1>0\\\lim\limits_{x\rightarrow-\infty}=-\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-\infty;-1\right)\)

Vậy pt đã cho có 3 nghiệm phân biệt với mọi m

Câu 2:

\(f'\left(x\right)=x^2+2\left(m-1\right)x+m+1\)

Để \(f'\left(x\right)\ge0\) \(\forall x\) \(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m+1\right)\le0\)

\(\Leftrightarrow m^2-3m\le0\Leftrightarrow0\le m\le3\)

Đúng(0)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 5 2019

Câu 3:

Nhận thấy \(x=0\) không phải nghiệm

\(\Leftrightarrow2x^3+3x^2-2=-mx\)

\(\Leftrightarrow\frac{2x^3+3x^2-2}{x}=-m\)

Đặt \(f\left(x\right)=\frac{2x^3+3x^2-2}{x}\Rightarrow f'\left(x\right)=\frac{\left(6x^2+6x\right)x-\left(2x^3+3x^2-2\right)}{x^2}=\frac{4x^3+3x^2+2}{x^2}\)

\(f'\left(x\right)=\frac{4x^2\left(x+1\right)+2-x^2}{x^2}\Rightarrow f'\left(x\right)>0\) \(\forall x\in\left(-1;1\right)\)

\(\Rightarrow f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\)

\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=+\infty\) ; \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=-\infty\)

\(\Rightarrow y=-m\) luôn cắt đồ thị \(y=f\left(x\right)\) hay phương trình đã cho luôn có ít nhất 1 nghiệm trong khoảng \(\left(-1;1\right)\) với mọi m

Đúng(0)
TC
Trân Châu
2 tháng 11 2021
KIỂM TRA 15'Câu 1: Tìm TXĐ của hàm số:    Câu 2: Giải các pt sau:a) b) c) Câu 3: Tìm m để pt sau có nghiệm: mn ui bày mk nha củm mơn mn nhìu  ...
Đọc tiếp

KIỂM TRA 15'

Câu 1: Tìm TXĐ của hàm số:    y equals fraction numerator sinx over denominator 1 minus sign 2 cosx end fraction

Câu 2: Giải các pt sau:

a) cos 2 italic x minus sign 1

b) square root of 3 italic c italic o italic t italic x minus sign 3 equals 0

c) 2 sin squared 2 x and sin 2 x minus sign 1 equals 0

Câu 3: Tìm m để pt sau có nghiệm:

square root of 3 sin italic x and 2 cos italic x equals italic m

smiley-laughing.gif mn ui bày mk nha củm mơn mn nhìu smiley-laughing.gif   
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021

Tất cả k dưới đây là \(k\in Z\)

1.

ĐKXĐ: \(1-2cosx\ne0\Rightarrow cosx\ne\dfrac{1}{2}\)

\(\Rightarrow x\ne\pm\dfrac{\pi}{3}+k2\pi\)

2.

\(cos2x-1=0\Rightarrow cos2x=1\)

\(\Rightarrow2x=k2\pi\)

\(\Rightarrow x=k\pi\)

b.

\(\sqrt{3}cotx-3=0\Rightarrow cotx=\sqrt{3}\)

\(\Rightarrow x=\dfrac{\pi}{6}+k\pi\)

c.

\(2sin^22x+sin2x-1=0\)

\(\Rightarrow\left[{}\begin{matrix}sin2x=-1\\sin2x=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{2}+k2\pi\\2x=\dfrac{\pi}{6}+k2\pi\\2x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)

3.

Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:

\(\sqrt{3}^2+2^2\ge m^2\)

\(\Rightarrow m^2\le7\)

\(\Rightarrow-\sqrt{7}\le m\le\sqrt{7}\)

Đúng(1)
TC
Trân Châu
2 tháng 11 2021

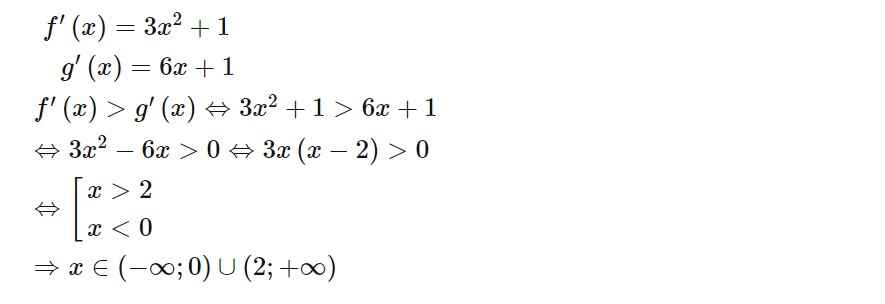
undefined

Đúng(0)
LT
Lynn Trang
22 tháng 5 2020

cho hàm số (c) có y=f(x) = x2-2x+3. viết phương trình tiếp tuyến với (c):

a) tại điểm thuộc (c) có hoành độ x0=1

b) song song với đường thẳng 4x-2y+5=0

c)vuông góc với đường thẳng x+4y=0

d)vuông góc với đường phân giác thứ nhất của góc hợp bởi các trục tọa độ
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 5 2020

\(f'\left(x\right)=2x-2\)

a/ \(f'\left(1\right)=0\) ; \(f\left(1\right)=2\)

Phương trình tiếp tuyến: \(y=2\)

b/ \(4x-2y+5=0\Leftrightarrow y=2x+\frac{5}{2}\)

Tiếp tuyến song song d nên có hệ số góc bằng 2

\(\Rightarrow2x_0-2=2\Rightarrow x_0=2\)

\(f\left(2\right)=3\)

Pt tiếp tuyến: \(y=2\left(x-2\right)+3=0\Leftrightarrow y=2x-1\)

c/ \(x+4y=0\Rightarrow y=-\frac{1}{4}x\)

Tiếp tuyến vuông góc d \(\Rightarrow\) có hsg k thỏa mãn \(k.\left(-\frac{1}{4}\right)=-1\Rightarrow k=4\)

\(\Rightarrow2x_0-2=4\Rightarrow x_0=3\) ; \(f\left(3\right)=6\)

Pt tiếp tuyến: \(y=3\left(x-3\right)+6=3x-3\)

d/ Đường phân giác góc phần thứ thứ nhất có pt \(y=x\)

\(\Rightarrow\) Tiếp tuyến có hệ số góc -1

\(\Rightarrow2x_0-2=-1\Rightarrow x_0=\frac{1}{2}\) ; \(f\left(\frac{1}{2}\right)=\frac{9}{4}\)

Pt: \(y=-1\left(x-\frac{1}{2}\right)+\frac{9}{4}=-x+\frac{11}{4}\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP