Lập bất phương trình cho bài toán sau :
Một ngân hàng đang thực hiện tỉ lệ lãi gửi tiết kiệm hàng tháng là 0,8%. Hỏi rằng, muốn có số tiền lãi hàng tháng ít nhất là 2 triệu đồng thì số tiền phải gửi tiết kiệm ít nhất là bao nhiêu tiền ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 12 2017
Gọi x (tính bằng triệu đồng) là số tiền gửi vào ngân hàng, ta có bất phương trình
x.0,8% ≥ 2.
10 tháng 2 2016
Giá vốn của tháng sau so với giá vốn của tháng liền trước là :
100 % + 1.9 % = 101.9%
Giá vốn của tháng thứ hai là :
6000000 x 101.9% = 6114000 ( đồng)
Giá vốn cuả tháng thứ ba là :
6114000 x 101.9% = 6230166 ( đồng )
Giá vốn và giá lãi của 3 tháng là :
6230166 x 101.9% = 6348539.154 ( đồng )
Đáp số : 6348539.154 đồng
30 tháng 12 2015
bài này mik suy nghĩ lại rồi kết quả là 963840 đồng đúng 100%
8 tháng 7 2021
Tiền lãi tháng đầu là:
60000000 x 0,8% = 480000 (đồng)
Tiền lãi tháng sau là:
(60000000 + 480000) x 0,8% = 483840 ( đồng )
Sau 2 tháng nhận được số tiền lãi là:
480000 + 483840 = 963840 (đồng)
HB
18 tháng 9
Tiền lãi tháng đầu là:
60000000 x 0,8% = 480000 (đồng)
Tiền lãi tháng sau là:
(60000000 + 480000) x 0,8% = 483840 ( đồng )
Sau 2 tháng nhận được số tiền lãi là:
480000 + 483840 = 963840 (đồng)
CM
13 tháng 11 2018
Áp dụng công thức lãi kép: 
Như vậy, khi gửi không kỳ hạn để được số tiền gồm cả vốn lẫn lãi lớn hơn hoặc bằng 300 triệu đồng thì ông A phải gửi tối thiểu là 100 tháng.
Nếu cũng gửi với số tiền ban đầu là 300 triệu đồng với lãi suất 1,2%/quý trong thời gian 100 năm (gồm 33 kỳ hạn và 1 tháng không kỳ hạn)
• Số tiền ông A có được sau định kỳ là: 
• Số tiền ông A có được sau 100 tháng là
NT
6 tháng 1 2016
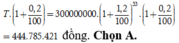
tháng 1 có số tiền lãi là
60000000*0,8/100=480000 đồng
tháng 2 có số tiền lãi là
(60000000+480000)/100*0,8=483840 đồng
cả 2 tháng lãi số tiền là
483840+480000=963840 đồng
6 tháng 1 2016
Tháng 1 lãi số tiền là :
60000000*0,8/100=480000 (đồng)
Tháng 2 lãi số tiền là :
(60000000+480000)/100*0,8=483840 (đồng)
Cả 2 tháng lãi số tiền là :
483840+480000=963840 (đồng)
Gọi x (tính bằng triệu đồng) là số tiền gửi vào ngân hàng.
Vì tỉ lệ lãi gửi tiết kiệm hàng tháng là 0,8% nên số tiền lãi hàng tháng là x.0,8%.
Ta có bất phương trình: x.0,8% ≥ 2