Giai hộ mình bài này vs. Mình cảm ơn trc nhé!
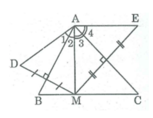
B1: Cho tam giác ABC có góc A= 70độ. điểm M thuộc cạnh BC. Vẽ điêm D đối xứng vs M qua AB, vẽ điểm E đối xứng vs M qua AC.
a) Chứng minh rằng AD=AE
b) Tính số đo góc DAE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2021
a: Ta có: D đối xứng với M qua AB
nên AD=AM(1)
Ta có: E đối xứng với M qua AC
nên AM=AE(2)
Từ (1) và (2) suy ra AD=AE
JK
21 tháng 9 2019
tự kẻ hình :
AB là đường trung trực của MD (gt)
=> AM = AD (đl) (1)
AC là đường trung trực của EM (gt)
=> AE = AM (đl) (2)
(1)(2) => AE = AD
21 tháng 9 2019
a. Vì D đối xứng với M qua trục AB
\(\Rightarrow\) AB là đường trung trực MD.
\(\Rightarrow\) AD = AM (tính chất đường trung trực) (1)
\(\Rightarrow\) Vì E đối xứng với M qua trục AC
\(\Rightarrow\) AC là đường trung trực của ME
\(\Rightarrow\) AM = AE ( tính chất đường trung trực) (2)
\(\Rightarrow\) Từ (1) và (2) suy ra : AD = AE
b ) AD = AM suy ra \(\Delta AMD\) cân tại A có \(AB\perp MD\)
nên AB cũng là đường phân giác của góc MAD
\(\Rightarrow\widehat{A_1}=\widehat{A}_2\)
AM = AE suy ra \(\Delta AME\) cân tại A có \(AC\perp ME\) nên AC cũng là đường phân giác của \(\widehat{MAE}\)
\(\Rightarrow\widehat{A}_3=\widehat{A}_4\)
\(\widehat{DAE}=\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+\widehat{A}_4\)
\(=2\left(\widehat{A}_2+\widehat{A}_3\right)=2\widehat{BAC}=2.70^o=140^o\)
Chúc bạn học tốt !!!
CM
9 tháng 2 2017
Vì D đối xứng với M qua trục AB
⇒ AB là đường trung trực của MD.
⇒ AD = AM (t/chất đường trung trực) (1)
Vì E đối xứng với M qua trục AC
⇒ AC là đường trung trực của ME
⇒ AM = AE (t/chất đường trung trực) (2)
Từ (1) và (2) suy ra: AD = AE
25 tháng 7 2016
Do lỗi Online Math nên mình không gửi câu trả lời được. Mình phải dùng paint .
22 tháng 9 2021
Cho tam giác ABC có góc B bằng 70 độ, điểm M thuộc cạnh AC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua BC. Chứng minh rằng tam giác BDE cân và tính góc DBE
Toán lớp 822 tháng 9 2021
a) M đối xứng với D qua AB nên MB=BD và AB vuông góc với MD. Ta thấy Am vừa là đường trung tuyến vừa là đường trung trực nên tam giác AMD cân ở A nên AM=AD
Tương tự ta chứng minh được tam giác AEM cân ở A nên AM=AE
=>AE=AD=AM
b)Gọi I là điểm giao của AB và MD, K là giao của AC và ME
tam giác AMD cân có AB là đường trung trực nên cũng là đường phân giác của góc MAD nên góc DAB=gócBAM
tam giác MAE cũng vậy nên góc MAC=gócEAC
vậy góc DAE=góc DAB+ góc BAM + góc MAC +góc CAE
= 2 (góc BAM+ goc MAC)
=2.70
=140 độ