Cho tam giác ABC vuông tại A, có đường cao AH. So sánh 13AB + 5 AC và 13 AH + 5 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2023
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: DH=DE
DE<DC
=>DH<DC
c: Xét ΔAKC có
CH,KE là đường cao
CH căt KE tại D
=>D là trực tâm
=>AD vuông góc KC
24 tháng 8 2023
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: ΔAHD=ΔAED
=>DH=DE
mà DE<DC
nên DH<DC
c: Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
góc HDK=góc EDC
=>ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
d: AH+HK=AK
AE+EC=AC
mà AH=AE và HK=EC
nên AK=AC
mà DK=DC
nên AD là trung trực của KC
mà M là trung điểm của CK
nên A,D,M thẳng hàng
12 tháng 7 2017
VẼ HÌNH HƠI XẤU THÔNG CẢM NHA
áp dụng hệ thức lượng trong tam giác vuông ABC ta có \(AB\cdot AC=AH\cdot BC\) \(\Rightarrow AH\cdot BC=63\) (1)
áp dụng đl pitagovao tam giác vuông ABC ta có \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{130}\)
thay vao (1) ta co \(AH\cdot BC=63\Rightarrow AH=\frac{63}{\sqrt{130}}\)
NA
2
8 tháng 7 2021
Áp dụng hẹ thức lượng trong tam giác vuông:
\(AB.AC=AH.BC=78\)
\(\Rightarrow AB=\dfrac{78}{AC}\)
Lại có:\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{78}{AC}\right)^2+AC^2=169\)
\(\Leftrightarrow AC^4-169AC^2+6084=0\)\(\Leftrightarrow\left[{}\begin{matrix}AC=\sqrt{117}=3\sqrt{13}\\AC=\sqrt{52}=2\sqrt{13}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}AB=2\sqrt{13}\\AB=3\sqrt{13}\end{matrix}\right.\)
Vậy \(AB=2\sqrt{13};AC=3\sqrt{13}\) hoặc \(AC=2\sqrt{13};AB=3\sqrt{13}\)
A
8 tháng 7 2021
Xét \(\Delta\)ABC vuông tại A, đường cao AH
\(AB.AC=AH.BC=6.13=78\)
\(\rightarrow AC=\dfrac{78}{AB}\)
Xét \(\Delta ABC\) vuông tại A
\(\rightarrow AB^2+AC^2=BC^2\left(Pytago\right)\)
\(\rightarrow AB^2+\left(\dfrac{78}{AB}\right)^2=13^2\)
\(\rightarrow AB^2+\dfrac{6084}{AB^2}=169\)
\(\rightarrow AB^4+6084=169AB^2\)
\(\rightarrow AB^4-169AB^2+6084=0\)
Đặt \(t=AB^2>0\). Phương trình trở thành:
\(t^2-169t+6084=0\)
\(\Leftrightarrow t^2-117t-52t+6084=0\)
\(\Leftrightarrow t\left(t-117\right)-52\left(t-117\right)=0\)
\(\Leftrightarrow\left(t-52\right)\left(t-117\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-52=0\\t-117=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=52\\t=117\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}AB^2=52\\AB^2=117\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AB=\sqrt{52}=2\sqrt{13}\rightarrow AC=\dfrac{78}{2\sqrt{13}}=3\sqrt{13}\\AB=\sqrt{117}=3\sqrt{13}\rightarrow AC=\dfrac{78}{3\sqrt{13}}=2\sqrt{13}\end{matrix}\right.\)
Vậy hai cạnh góc vuông của tam giác vuông là \(3\sqrt{13}\) và \(2\sqrt{13}\)
TT
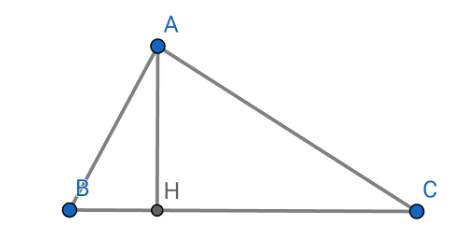
cho tam giác ABC vuông tại A , đường cao AH . so sánh BC+AH và AB+AC
BÀI NÀY KHÓ QUÁ GIÚP MK VỚI HUHU
2
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
ND
0