Cho đường tròn (O), bán kính OA, dây CD là đường trung trục của OA
a) Tứ giác OCAD là hình gì ? Vì sao ?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến nàu cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Đồng thời CD ⊥ OA nên ACOD là hình thoi.
b) Vì ACOD là hình thoi nên AC = OC
Mà OC = OA ( = R) nên tam giác OAC đều
Suy ra: ^COA=60∘COA^=60∘ hay ˆCOI=60∘
Mà CI ⊥ OC (tính chất tiếp tuyến)
Trong tam giác vuông OCI, ta có:
CI=OC.tgˆCOI=R.tg60∘=R√3CI=OC.tgCOI^=R.tg60∘=R3.

a,b: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
Xét tứ giác OBAC có
H là trung điểm chung của OA và BC
OB=OC
Do đó: OBAC là hình thoi
=>OB=BA=OA
=>ΔOAB đều
=>góc BOA=60 độ
Xét ΔOBM vuông tại B có tan BOM=BM/BO
=>BM/6=tan 60
=>\(BM=6\sqrt{3}\left(cm\right)\)
c: Xét ΔOBM và ΔOCM có
OB=OC
góc BOM=góc COM
OM chung
Do đó: ΔOBM=ΔOCM
=>góc OCM=90 độ
=>MC là tiếp tuyến của (O)

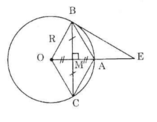
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều = > ∠ A O B = 60 °
Trong tam giác OBE vuông tại B ta có:
B E = O B . t g ∠ A O B = O B . t g 60 ° = R . √ 3


a) Xét tam giác vuông $MBO$ vuông tại $B$ có đường cao $BH$:
\(\frac{1}{BH^2}=\frac{1}{MB^2}+\frac{1}{BO^2}=\frac{1}{BO^2-HO^2}\)\(\Rightarrow \frac{1}{MB^2}=\frac{1}{27}-\frac{1}{36}=\frac{1}{108}\Rightarrow MB=6\sqrt{3} (\text{cm})\)
b) Thấy rằng $BC$ là trung trực của $AO$ và $AO$ cũng là trung trực của $BC$ nên $BA=BO=OC=AC$
Mặt khác \(\cos(\widehat{BOH})=\frac{1}{2}\) nên \(\cos (\widehat{BOC})\neq 90^0\)
Do đó $OBAC$ là hình thoi
c) Vì $OA$ là trung trực của $BC$ nên với điểm $M\in OA$ thì $MB=MC$ suy ra \(\triangle MBO=\triangle MCO\Rightarrow \widehat {MBO}=\widehat{MCO}=90^0\Rightarrow MC\perp CO\)
Do đó $MC$ là tiếp tuyến của $(O)$

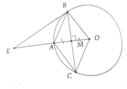
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3