Tìm số điểm biểu diễn của số phức z sao cho \(z^4\) - 1 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
14 tháng 11 2018
Đáp án A
Giả sử ![]()
Ta có M(a;b) và M'(a;-b)
Khi đó ![]()
Suy ra ![]() và
và ![]()
Do 4 điểm M, N, M’, N’ tạo thành hình thang cân nhận Ox làm trục đối xứng nên 4 điểm đó lập thành hình chữ nhật
![]()

Với a = -b, ta có
![]()
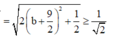
Dấu bằng xảy ra khi 
Với  ta có
ta có 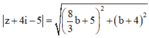
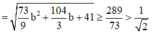
Vậy 

NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2021
\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
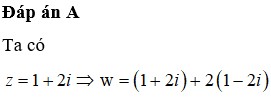

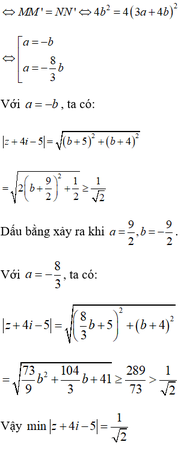

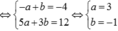


gọi \(z=a+bi\) với \(\left(a;b\in Z;i^2=-1\right)\)
ta có : \(z^4-1=0\Leftrightarrow\left(a+bi\right)^4-1=0\)
\(\Leftrightarrow a^4+4a^3bi+6a^2b^2i^2+4ab^3i^3+b^4i^4-1=0\)
\(\Leftrightarrow a^4+4a^3bi-6a^2b^2-4ab^3i+b^4-1=0\)
\(\Leftrightarrow\left(a^4-6a^2b^2+b^4-1\right)+\left(4a^3b-4ab^3\right)i=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^4-6a^2b^2+b^4-1=0\\4a^3b-4ab^3=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4ab\left(a-b\right)\left(a+b\right)=0\\a^4-6a^2b^2+b^4-1=0b+++b^4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\b=0\\a=b\\a=-b\end{matrix}\right.\\a^4-6a^2b^2+b^4-1=0\end{matrix}\right.\)
với \(a=0\Rightarrow b=\pm1\)
với \(b=0\Rightarrow a=\pm1\)
với \(a=b\Rightarrow\)\(vônghiệm\)
với \(a=-b\Rightarrow\) \(vônghiệm\)
\(\Rightarrow z=1;z=-1;z=i;z=-i\)
vậy có 4 điểm biểu diển của số phức \(z\)