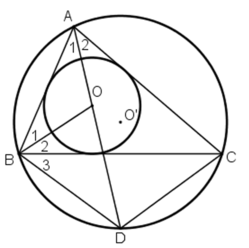
Cho tam giác ABC nội tiếp đường tròn (O') và ngoại tiếp đường tròn (O). Tia AO cắt đường tròn (O') tại D. Ta có :
(A) CD = BD = O'D
(B) AO = CO = OD
(C) CD = CO = BD
(D) CD = OD = BD
Hãy chọn câu trả lời đúng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2017
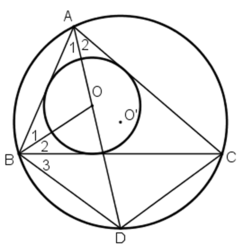
Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.
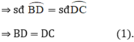
(hai cung bằng nhau căng hai dây bằng nhau).
+ 
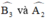đều là các góc nội tiếp chắn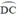 
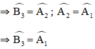
ΔOAB có 
là góc ngoài của tam giác
Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.
CM
10 tháng 10 2017
Do O là tâm đường tròn nội tiếp tam giác ABC nên O là giao điểm của ba đường phân giác của tam giác ABC.
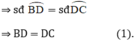
(hai cung bằng nhau căng hai dây bằng nhau).
+ 
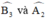đều là các góc nội tiếp chắn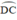 
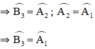
ΔOAB có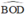 
là góc ngoài của tam giác
Từ (1) và (2) suy ra DB = DC = DO.
Vậy chọn đáp án D.
Hướng dẫn làm bài:
Vì AC vad BC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:
ˆCAD=ˆBAD=αCAD^=BAD^=α (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)
⇒ cung CD = cung DB ⇒CD = DB (*)
Tương tự, CO là tia phân giác của góc C nên:
ˆACO=ˆBCO=βACO^=BCO^=β
Mặt khác: ˆDCO=ˆDCB+ˆBCO=α+β(1)(doˆBAD=ˆBCDDCO^=DCB^+BCO^=α+β(1)(doBAD^=BCD^
Ta có: ˆCODCOD^ là góc ngoài của ∆ AOC nên
ˆCOD=ˆOAC+ˆOCA=β+α(2)COD^=OAC^+OCA^=β+α(2)
Từ (1) và (2) ta có: ˆOCD=ˆCODOCD^=COD^
Vậy ∆DOC cân tại D (**)
Từ (*) và (**) suy ra CD = OD = BD
Chọn đáp án D