Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm \(A\left(-1;-1\right),B\left(-1;-2\right),C\left(\sqrt{2},\sqrt{2}\right)\) đối với đường tròn tâm O bán kính 2 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


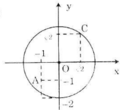
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
OC2 = (√2)2 + (√2)2 = 4 => OC = 2 = R
=> C nằm trên (O)

Gọi R là bán kính của đường tròn (O; 2). Ta có: R = 2
O A 2 = 1 2 + 1 2 = 2 ⇒ OA = 2 < 2
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
O B 2 = 2 2 + 2 2 = 2 + 2 = 4 ⇒ OB = 2
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
O C 2 = 1 2 + 2 2 = 1 + 4 = 5 ⇒ OC = 5 > 2

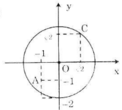
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
O C 2 = ( √ 2 ) 2 + ( √ 2 ) 2 = 4 = > O C = 2 = R
=> C nằm trên (O)

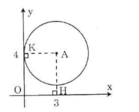
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

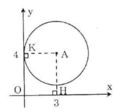
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy

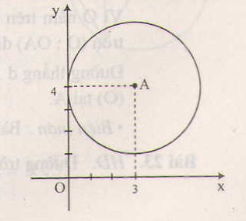
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.

- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.
Khoảng cách d từ gốc tọa độ đến điểm (x;y) được tính theo công thức d=√x2+y2d=x2+y2
Ta có OA=√2<2⇒AOA=2<2⇒A nằm trong đường tròn (O;2).
OB=√5>2⇒BOB=5>2⇒B nằm ngoài đường tròn (O;2).
OC=2⇒COC=2⇒C nằm trên đường tròn (O;2).