tam giác abc vuông tại a có đường cao ah, trung tuyến am. biết ab=5cm, bc=13cm. gọi d,e là hình chiếu của điểm h trên cạnh ab,ac. chứng minh bd/ce=(ab/ac)^3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2021
Trả lời:
a, ta có AB^2+AC^2=5^2+12^2=25+144=169
BC^2=13^2=169
=>AB^2+AC^2=BC^2
=>tam giác ABC vuông tại A( định lí pytago đảo)
b, ta có AH ⊥BC
=> tam giác AHB và tam giác AHC vuông tại H
+tam giác AHC có HF là đường cao
=> AH^2=AF.AC(1)
+tam giác AHB có HE là đường cao
=> AH^2=AE.AB(2)
từ(1) và (2)=> AF.AC=AE.AB(=AH^2)
c, ta có AH là đường cao của tam giác ABC
=>AH ⊥BC(*)
+{ HE ⊥AB=> góc HEA=90*
+{HF ⊥AC=>góc HFA=90*
+{AB ⊥AC=> góc BAC=90*
=> tứ giác AEHF là hình chữ nhật
lại có AH và EF là đường chéo
=> AH ⊥EF(**)
từ (*)(**) => EF//BC
=> góc AEF=góc ABC(đồng vị)
ΔABC ∞ ΔAEF(g.g) vì
góc A chung
góc ABC=góc AEF(cmt)
=>đpcm
Đúng thì k sai thì cho mik xin lỗi
HT
18 tháng 8 2021
a, ta có AB^2+AC^2=5^2+12^2=25+144=169
BC^2=13^2=169
=>AB^2+AC^2=BC^2
=>tam giác ABC vuông tại A( định lí pytago đảo)
b, ta có AH ⊥BC
=> tam giác AHB và tam giác AHC vuông tại H
+tam giác AHC có HF là đường cao
=> AH^2=AF.AC(1)
+tam giác AHB có HE là đường cao
=> AH^2=AE.AB(2)
từ(1) và (2)=> AF.AC=AE.AB(=AH^2)
c, ta có AH là đường cao của tam giác ABC
=>AH ⊥BC(*)
+{ HE ⊥AB=> góc HEA=90*
+{HF ⊥AC=>góc HFA=90*
+{AB ⊥AC=> góc BAC=90*
=> tứ giác AEHF là hình chữ nhật
lại có AH và EF là đường chéo
=> AH ⊥EF(**)
từ (*)(**) => EF//BC
=> góc AEF=góc ABC(đồng vị)
ΔABC ∞ ΔAEF(g.g) vì
góc A chung
góc ABC=góc AEF(cmt)
=>đpcm
29 tháng 10 2021
b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
4 tháng 4 2021
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(Gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{AB}{3}=\dfrac{BC}{5}\)
Ta có: AD+CD=AC(D nằm giữa A và C)
nên AC=3+5=8(cm)
Đặt \(\dfrac{AB}{3}=\dfrac{BC}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=3k\\BC=5k\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\left(3k\right)^2+8^2=\left(5k\right)^2\)
\(\Leftrightarrow9k^2+64=25k^2\)
\(\Leftrightarrow16k^2=64\)
\(\Leftrightarrow k^2=4\)
hay k=2
Suy ra: \(\left\{{}\begin{matrix}AB=3\cdot k=3\cdot2=6\left(cm\right)\\BC=5\cdot k=5\cdot2=10\left(cm\right)\end{matrix}\right.\)
Vậy: AB=6cm; BC=10cm
23 tháng 10 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)
b: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
Do đó: ΔAEF đồng dạng với ΔACB
c: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)
ΔBAD vuông tại A có
\(cotABD=\dfrac{AB}{AD}\)(2)
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)
18 tháng 12 2023
a:
Sửa đề: Là hình chiếu của H trên AB,AC
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Ta có: MA=MC
=>\(\widehat{MAC}=\widehat{MCA}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAD}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
\(\widehat{AED}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM\(\perp\)DE
c: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Ta có: ADHE là hình chữ nhật
=>AH=DE
mà AH=4,8cm
nên DE=4,8cm
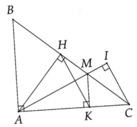
ta có : \(\Delta BDH~\Delta BAC\Rightarrow\frac{BD}{DH}=\frac{BA}{AC}\)
ta có : \(\Delta DHA~\Delta ABC\Rightarrow\frac{HD}{DA}=\frac{AB}{AC}\) và \(\Delta CHE~\Delta CAB\Rightarrow\frac{CH}{HE}=\frac{AB}{AC}\)
nhâm ba đẳng thức lại ta có :
\(\frac{BD}{DH}.\frac{DH}{DA}.\frac{HE}{CE}=\left(\frac{AB}{AC}\right)^3\) mà DA=HE ( do DAEH là hình chữ nhậy)
nên \(\frac{BD}{CE}=\left(\frac{AB}{AC}\right)^3\)