Giải các bất phương trình và biểu diễn tập nghiệm trên trục số :
a) \(1,2x< -6\)
b) \(3x+4>2x+3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 11 2017
1,2x < -6
⇔1,2 x : 1,2 < -6 : 1,2
⇔ x < - 5
Vậy nghiệm của bất phương trình là x < -5.
23 tháng 4 2022
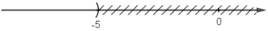
A, 3X+6>0
(=)3X>-6
(=)X>-2
VẬY ...
B,10-2X≥-4
(=)-2X≥-4-10
(=)-2X≥-14
(=)X≤7
VẬY....
C,
(=)
(=) -15X+10>-3+3X
(=)-15X-3X>-3-10
(=)-18X>-13
(=)X<
10 tháng 4 2018
a) 1,2x < -6
\(\Leftrightarrow1,2x.\dfrac{1}{1,2}< -6.\dfrac{1}{1,2}\)
\(\Leftrightarrow\) \(\dfrac{1,2x}{1,2}< \dfrac{-6}{1,2}\)
\(\Leftrightarrow x< -5\)
Vậy nghiệm của BPT là : \(x< -5\)
b) \(3x+4>2x+3\)
\(\Leftrightarrow3x-2x>-4+3\)
\(\Leftrightarrow x>-1\)
Vậy nghiệm của BPT là : \(x>-1\)
c) \(2x-3>0\)
\(\Leftrightarrow2x>3\)
\(\Leftrightarrow2x.\dfrac{1}{2}>3.\dfrac{1}{2}\)
\(\Leftrightarrow x>1,5\)
Vậy nghiệm của BPT là : \(x>1,5\)
d) \(4-3x\le2\)
\(\Leftrightarrow-3x\le2-4\)
\(\Leftrightarrow-3x\le-2\)
\(\Leftrightarrow-3x.\dfrac{-1}{3}\ge-2.\dfrac{-1}{3}\)
\(\Leftrightarrow x\ge\dfrac{2}{3}\)
Vậy tập nghiệm của BPT là : \(x\ge\dfrac{2}{3}\)
12 tháng 5 2023
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
d: =>3x>=9
=>x>=3
PT
1
CM
20 tháng 1 2019
3x + 4 > 2x + 3
⇔ 3x - 2x > 3 - 4 (chuyển vế 2x và 4, đổi dấu hạng tử).
⇔ x > -1
Vậy nghiệm của bất phương trình là x > -1.
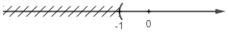
a) 1,2x < -6 \(\Leftrightarrow\)x < -6 : 1,2 \(\Leftrightarrow\) x < - 5
Vậy tập nghiệm của bất phương trình là S = {x | x < -5}
b) 3x + 4 > 2x + 3
⇔ 3x - 2x > 3 - 4 \(\Leftrightarrow\) x > -1
Vậy tập nghiệm của bất phương trình là S = {x | x > -1}