giải dùm mình mấy câu khoanh tròn đi ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2022
5/ \(10x+3-5x\le14x+12\)
<=>\(10x-5x-14x\le12-3\)
<=>\(-9x\le9\)
<=>\(x\ge-1\)
Vậy bất phương trình có nghiệm là \(x\ge-1\)
1 tháng 4 2022
6/\(\left(3x-1\right)< 2x+4\)
<=>\(3x-2x< 4+1\)
<=> x<5
Vậy tập nghiệm của bất phương trình là x<5
25 tháng 12 2023
Bài 3:
2:
a: Thay m=0 vào (d), ta được:
\(y=\left(0+1\right)x-2=x-2\)
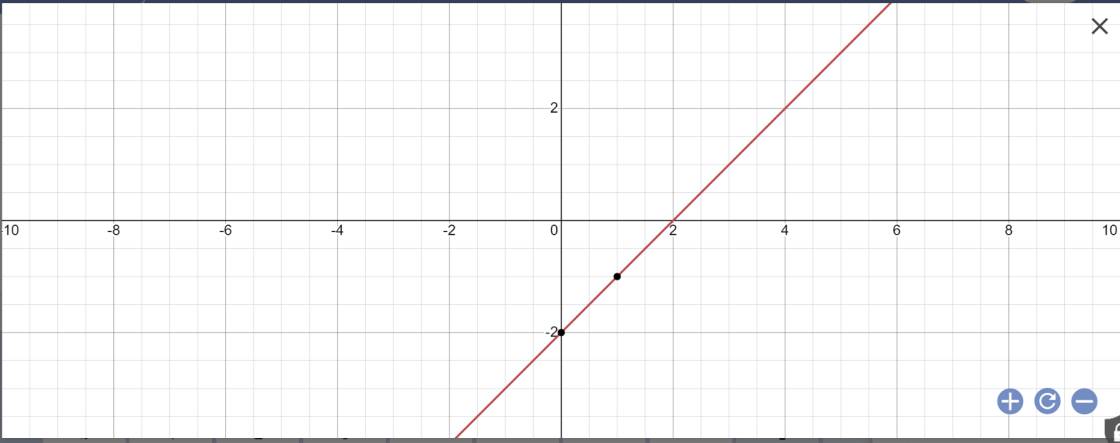
b: Thay x=1 vào y=x+1, ta được:
y=1+1=2
Thay x=1 và y=2 vào (d), ta được:
1(m+1)-2=2
=>m+1=4
=>m=3
c: Để \(\widehat{OAB}=45^0\) thì góc tạo bởi (d) với trục Ox bằng 45 độ
(d): y=(m+1)x-2
=>a=m+1
\(\Leftrightarrow tanOAB=a=m+1\)
=>m+1=tan45=1
=>m=0
BB
1
6 tháng 1 2023
Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2
3 tháng 8 2023
1. should ask
*must not ask là sai vì người quản lí mới nên hỏi vài câu hỏi trước khi thực hiện thay đổi
*have to ask (mang tính chủ quan) nên có làm hay không làm cũng được nên ta không chọn đáp án này
2. could prevent
Vì sau would, could là V_inf
NH
các ban làm mấy câu khoanh tròn giúp mình với nhé mấy câu lũy thừa mình không hiểu lắm
3
H
26 tháng 9 2023
Bài `3`
Cậu tách cho các câu sau nx nhé^^
\(a,x+\dfrac{1}{2}=\dfrac{7}{3}\\ \Rightarrow x=\dfrac{7}{3}-\dfrac{1}{2}\\ \Rightarrow x=\dfrac{14}{6}-\dfrac{3}{6}\\ \Rightarrow x=\dfrac{11}{6}\\ b,\dfrac{2}{5}x-\dfrac{1}{5}=-0,6\\ \Rightarrow\dfrac{2}{5}x=-\dfrac{3}{5}+\dfrac{1}{5}\\ \Rightarrow\dfrac{2}{5}x=-\dfrac{2}{5}\\ \Rightarrow x=-\dfrac{2}{5}:\dfrac{2}{5}\\ \Rightarrow x=-1\\ c,\left(0,5x-\dfrac{3}{7}\right):\dfrac{1}{2}=1\dfrac{1}{7}\\ \Rightarrow\dfrac{1}{2}x-\dfrac{3}{7}=\dfrac{8}{7}\cdot\dfrac{1}{2}\\ \Rightarrow\dfrac{1}{2}x-\dfrac{3}{7}=\dfrac{8}{14}\\ \Rightarrow\dfrac{1}{2}x=\dfrac{4}{7}+\dfrac{3}{7}\\ \Rightarrow\dfrac{1}{2}x=1\\ \Rightarrow x=1:\dfrac{1}{2}\\ \Rightarrow x=2\)
\(d,\dfrac{2}{3}x-\dfrac{2}{5}=\dfrac{1}{2}x-\dfrac{1}{3}\\ \Rightarrow\dfrac{2}{3}x-\dfrac{1}{2}x=-\dfrac{1}{3}+\dfrac{2}{5}\\ \Rightarrow\left(\dfrac{2}{3}-\dfrac{1}{2}\right)x=\dfrac{1}{15}\\ \Rightarrow\dfrac{1}{6}x=\dfrac{1}{15}\\ \Rightarrow x=\dfrac{1}{15}:\dfrac{1}{6}\\ \Rightarrow x=\dfrac{2}{5}\)
`e,1/2 x+2 1/2=3 1/2 x-3/4`
`=> 1/2 x+ 5/2= 7/2x - 3/4`
`=> 1/2x - 7/2x = -3/4 -5/2`
`=> -3x=-13/4`
`=>x=13/12`
\(f,2x\left(x-\dfrac{1}{7}\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x-\dfrac{1}{7}=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{7}\end{matrix}\right.\\ g,\left(\dfrac{2x}{5}-1\right):\left(-5\right)=\dfrac{1}{4}\\ \Rightarrow2x:5-1=\dfrac{1}{4}\cdot\left(-5\right)\\ \Rightarrow2x:5-1=-\dfrac{5}{4}\\ \Rightarrow2x:5=-\dfrac{5}{4}+1\\ \Rightarrow2x:5=-\dfrac{1}{14}\\ \Rightarrow2x=-\dfrac{1}{14}\cdot5\\ \Rightarrow2x=-\dfrac{5}{14}\\ \Rightarrow x=-\dfrac{5}{14}:2\\ \Rightarrow x=-\dfrac{5}{28}\)
\(\left(x-1\right)^3=\dfrac{1}{8}\\ \Rightarrow\left(x-1\right)^3=\left(\dfrac{1}{2}\right)^3\\ \Rightarrow x-1=\dfrac{1}{2}\\ \Rightarrow x=\dfrac{1}{2}+1\\ \Rightarrow x=\dfrac{1}{2}+\dfrac{2}{2}\\ \Rightarrow x=\dfrac{3}{2}\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
NT
Cho mik hỏi mấy câu khoanh tròn ạ. Mik cần gấp trước 12h trưa ngày mai
2
AT
18 tháng 7 2021
13) để căn thức xác định \(\Rightarrow\dfrac{2x-4}{-2}\ge0\) mà \(-2< 0\Rightarrow2x-4\le0\)
\(\Rightarrow x-2\le0\Rightarrow x\le2\)
14) để căn thức xác định \(\Rightarrow-\dfrac{2}{x-2}\ge0\Rightarrow\dfrac{2}{x-2}\le0\)
mà \(2>0\Rightarrow x-2< 0\Rightarrow x< 2\)
15) để căn thức xác định \(\Rightarrow\dfrac{2\sqrt{15}-\sqrt{59}}{7-x}\ge0\)
Ta có: \(2\sqrt{15}=\sqrt{60}>\sqrt{59}\left(60>59\right)\Rightarrow2\sqrt{15}-\sqrt{59}>0\)
\(\Rightarrow7-x>0\Rightarrow x< 7\)
3) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}1-x\ge0\\3-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le1\\x\le3\end{matrix}\right.\Rightarrow x\le1\)
4) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}15-3x\ge0\\5-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le5\\x\le5\end{matrix}\right.\Rightarrow x\le5\)
5) để căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}3x-9\ge0\\9-x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge3\\x\le9\end{matrix}\right.\Rightarrow3\le x\le9\)
18 tháng 7 2021
Bài 1:
1) \(\sqrt{2}< \sqrt{3}\)
2) \(\sqrt{3}< \sqrt{10}\)
3) \(2\sqrt{3}>2\sqrt{2}\)
4) \(3\sqrt{3}< 3\sqrt{5}\)
5) \(5\sqrt{2}>3\sqrt{2}\)
6) \(-5\sqrt{3}< -3\sqrt{3}\)
Dạng 2d)
4FeS2+11O2=2Fe2O3+8SO2( điểu kiện nhiệt độ)
SO2+2H2S=3S+2H2O( điểu kiện nhiệt độ)
S+Fe=FeS( điểu kiện nhiệt độ)
FeS+H2SO4=FeSO4+H2S
2H2S+3O2=2SO2+2H2O
SO2+2NaOH=Na2SO3+H2O
Na2SO3+H2SO4=Na2SO4+SO2+H2O
SO2+Br2+2H2O=H2SO4+2HBr