Hình 61 cho biết a // b, \(\widehat{C}=44^0;\widehat{D}=132^0\)
Tính số đo góc COD

(Hướng dẫn : Vẽ đường thẳng song song với đường thẳng a và đi qua điểm O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) Ta có: AB // CD, CD _|_ a
\(\Rightarrow\) AB _|_ a
\(\Rightarrow\widehat{A}=90^o\)
b) Vì AB // CD nên:
\(\widehat{C_1}=\widehat{B_4}=61^o\) ( đồng vị )
\(\Rightarrow\widehat{B_4}=\widehat{B_2}=61^o\) ( đối đỉnh )
\(\Rightarrow\widehat{B_1}+\widehat{B_2}=180^o\) ( kề bù )
Mà \(\widehat{B_2}=61^o\Rightarrow\widehat{B_1}=119^o\)
\(\Rightarrow\widehat{B_1}=\widehat{C_2}=161^o\) ( đồng vị )
Vậy a) \(\widehat{A}=90^o\)
b) \(\widehat{B_2}=61^o,\widehat{B_1}=119^o,\widehat{C_2}=119^o\)
Hình vẽ có rồi nha!!!!!!
a) Vì AB // CD (gt)
\(\Rightarrow\)\(\widehat{D} = \widehat{A}\) (so le trong)
mà \(\widehat{D} = 90^0\) (gt)
\(\Rightarrow\)\(\widehat{A} = 90^0\)
b) Ta có:
\(\widehat{C1} + \widehat{C2} = 180^0\) (kề bù)
\(61^0+ \widehat{C2} = 180^0 (\widehat{C1} = 61^0(gt))\)
\(\widehat{C2} = 119^0\)
Vì AB // CD (gt)
\(\Rightarrow\) \(\widehat{C2} = \widehat{B1} = 119^0\) (đồng vị)
\(\widehat{B2} = \widehat{C1} = 61^0\) (so le ngoài)

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

a) Vì a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\); \(\widehat {{M_4}} = \widehat {{N_4}}\) ( 2 góc đồng vị) mà \(\widehat {{N_3}} = \widehat {{N_1}}\) ; \(\widehat {{N_4}} = \widehat {{N_2}}\) ( 2 góc đối đỉnh) nên \(\widehat {{M_1}}\) =\(\widehat {{N_3}}\); \(\widehat {{M_4}}\) =\(\widehat {{N_2}}\)
b) Vì a // b nên \(\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}\) ( 2 góc đồng vị), mà \(\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{M_2}} + \widehat {{N_1}}\) = 180\(^\circ \); \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180\(^\circ \)
Chú ý:
Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau
+ Hai góc trong cùng phía có tổng số đo bằng 180\(^\circ \)

Tham khảo:
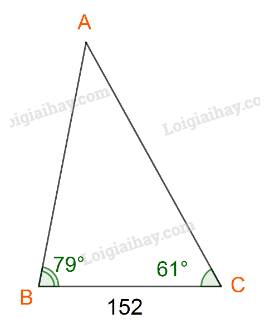
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{2\sin A}} = \frac{{152}}{{2\sin {{40}^o}}} \approx 118,235\end{array}\)
Vẽ tia Ot // a (Ca, Ot nằm ở hai nửa mp đối nhau có bờ OC).
ˆCOD=ˆCOt+ˆDOtCOD^=COt^+DOt^
Mà a // Ot
=> ˆCOt=1800−ˆOPbCOt^=1800−OPb^
(hai góc trong cùng phía)
Suy ra: ˆtOD=1800−1320=480tOD^=1800−1320=480
Vậy ˆCOD=440+480=920