Một cách chứng minh khác của định lí 1 :
Cho tam giác ABC với AC >AB. Trên tia AC, lấy điểm B' sao cho AB' = BA
a) Hãy so sánh góc ABC với góc ABB'
b) Hãy so sánh góc ABB' với góc AB'B
c) Hãy so sánh góc AB'B với góc ACB
Từ đó suy ra \(\widehat{ABC}=\widehat{ACB}\)

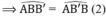
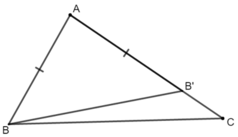
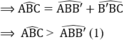
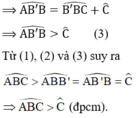
a) Trên tia AC, AB' = AB
mà AB < AC ( giả thiết)
nên B' nằm giữa hai tia BA và BC
=> tia BB' nằm giữa hai tia BA và BC
=> ˆABB′<ˆABCABB′^<ABC^
b) ∆ABB' có AB = AB' nên cân tại A
=> ˆABB′<ˆAB′BABB′^<AB′B^
c) Vì là góc ngoài tại B' của ∆BB'C nên ˆABB′<ˆACBABB′^<ACB^
Vì ˆABB′<ˆABCABB′^<ABC^ (câu a)
ˆABB′<ˆAB′BABB′^<AB′B^ (câu b)
ˆABB′<ˆACBABB′^<ACB^ (câu c)
=> ˆABC<ˆACB