Cho tam giác ABC vuông tại A, đường cao AH=24cm. Biết AB:AC=3:4. Tính độ dài các cạnh của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9 2016
AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm
27 tháng 7 2017
B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia
AH
Akai Haruma
Giáo viên
11 tháng 7 2023
Lời giải:
Do $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{144}=\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{25}{144a^2}$
$\Rightarrow a^2=25\Rightarrow a=5$ (do $a>0$)
$\Rightarrow AB=3a=15; AC=4a=20$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm) - theo định lý Pitago
CM
11 tháng 12 2017
Sử dụng hệ thức về cạnh góc vuông và đường cao trong tam giác vuông, tính được BH =4,5cm, CH = 8cm
CM
9 tháng 5 2018
Đáp án A
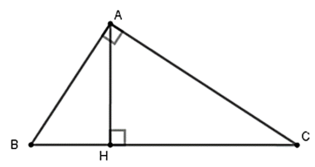
Ta có AB:AC = 3:4, đặt AB = 3a; AC = 4a (a > 0)
Theo hệ thức về cạnh và đường cao trong tam giác vuông AHC ta có:
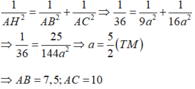
Theo định lý Pytago cho tam giác vuông ta có:
29 tháng 4 2020
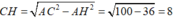
Mình làm mẫu cho bạn câu a) nhé
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé
2 tháng 2 2022
Bài 1:
a: \(AB=21\cdot\dfrac{3}{7}=9\left(cm\right)\)
AC=21-9=12(cm)
=>BC=15(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=7,2(cm)
Xét ΔAHB vuông tại H có \(AB^2=AH^2+BH^2\)
hay BH=5,4(cm)
=>CH=9,6(cm)
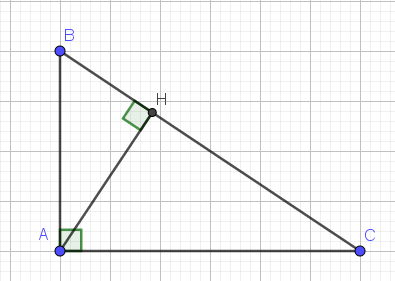
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(AB=\dfrac{3}{4}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{16}AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{576}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{16}=576\cdot\dfrac{25}{16}=900\)
\(\Leftrightarrow AC^2=1600\left(cm\right)\)
\(\Leftrightarrow AC=40\left(cm\right)\)
\(\Leftrightarrow AB=30\left(cm\right)\)
\(\Leftrightarrow BC=50cm\)