Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng hệ thức về cạnh góc vuông và đường cao trong tam giác vuông, tính được BH =4,5cm, CH = 8cm

B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia

Đáp án A
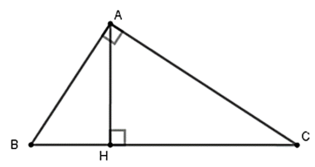
Ta có AB:AC = 3:4, đặt AB = 3a; AC = 4a (a > 0)
Theo hệ thức về cạnh và đường cao trong tam giác vuông AHC ta có:
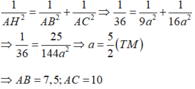
Theo định lý Pytago cho tam giác vuông ta có:
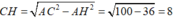

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

AB/AC=5/6
=>BH/CH=25/36
=>BH/25=CH/36=k
=>BH=25k; CH=36k
AH^2=HB*HC
=>900k^2=12^2=144
=>k=2/5
=>BH=10cm; CH=14,4cm

a: AC=căn 5^2-3^2=4cm
AH=3*4/5=2,4cm
BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: \(BH=\sqrt{60^2:144}=5\left(cm\right)\)
BC=144+5=149cm
\(AB=\sqrt{5\cdot149}=\sqrt{745}\left(cm\right)\)
\(AC=\sqrt{144\cdot149}=12\sqrt{149}\left(cm\right)\)
c: \(HC=\sqrt{AC^2-AH^2}=\dfrac{144}{13}\left(cm\right)\)
\(BH=\dfrac{AH^2}{HC}=\dfrac{25}{13}cm\)
BC=BH+CH=13(cm)
AB=căn 13^2-12^2=5cm
a
Áo dụng đl pytago vào tam giác ABC vuông tại A:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
\(CH=BC-BH=5-1,8=3,2\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{3.4}{5}=2,4\left(cm\right)\)
b
Áp dụng đl pytago vào tam giác AHC vuông tại H có:
\(AC=\sqrt{AH^2+HC^2}=\sqrt{60^2+144^2}=156\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC vuông tại A, đường cao AH có:
\(AC^2=HC.BC\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{156^2}{144}=169\left(cm\right)\)
\(BH=BC-HC=169-144=25\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{25.169}=65\left(cm\right)\)
c
Áp dụng đl pytago vào tam giác AHC vuông tại H:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{12^2-\left(\dfrac{60}{13}\right)^2}=\dfrac{144}{13}\approx11,08\left(cm\right)\)
Theo hệ thức lượng vào tam giác ABC đường cao AH có:
\(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{\left(\dfrac{60}{13}\right)^2}{\dfrac{144}{13}}=\dfrac{25}{13}\approx1,92\left(cm\right)\)
\(BC=HB+HC=\dfrac{25}{13}+\dfrac{144}{13}=13\left(cm\right)\)
\(AB^2=HB.BC\Rightarrow AB=\sqrt{HB.HC}=\sqrt{\dfrac{144}{13}.\dfrac{25}{13}}=\dfrac{60}{13}\approx4,62\left(cm\right)\)


Lời giải:
Do $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{144}=\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{25}{144a^2}$
$\Rightarrow a^2=25\Rightarrow a=5$ (do $a>0$)
$\Rightarrow AB=3a=15; AC=4a=20$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm) - theo định lý Pitago
Hình vẽ: