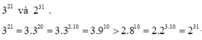Giải dùm em bài toán so sánh : 231 và 321
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
2
13 tháng 3 2016
ta thấy:11/54=22/108
vì 108> 37
=> 22/108< 22/37
hay 11/54< 22/37
HM
1
4 tháng 11 2015
Ta có:
2225 = (29)25 = 51225
3150 = (36)25 = 72925
Vì 51225 < 72925 => 2225 < 3150
BD
3
5 tháng 10 2017
\(9^{35}=\left(3^2\right)^{35}=3^{70}\)
VÌ \(3^{60}< 3^{70}\)
NÊN \(3^{60}< 9^{35}\)
5 tháng 10 2017
Ta có :
\(9^{35}=\left(3^2\right)^{35}=3^{70}\)
Vì \(3^{60}< 3^{70}\Rightarrow3^{60}< 9^{35}\)
Vậy\(3^{60}< 9^{35}\)
6 tháng 10 2018
Ta có:
\(\frac{932}{1023}=1-\frac{91}{1023}\)
\(\frac{876}{997}=1-\frac{121}{997}\)
Ta thấy: \(\frac{121}{997}>\frac{91}{997}>\frac{91}{1023}\)
\(\Rightarrow1-\frac{91}{1023}>1-\frac{121}{997}\)
\(\Rightarrow\frac{932}{1023}>\frac{876}{997}\)
11 tháng 9 2021
\(3^{21}=3^{20}.3=9^{10}.3\)
\(2^{31}=2^{30}.2=8^{10}.2\)
Do \(9^{10}>8^{10},3>2\)
\(\Rightarrow9^{10}.3>8^{10}.2\Rightarrow3^{21}>2^{31}\)
11 tháng 9 2021
\(3^{21}=3^{20}\cdot3\)
\(2^{31}=2^{30}\cdot2\)
mà \(3^{20}>2^{30}\)
nên \(3^{21}>2^{31}\)
CM
14 tháng 10 2017
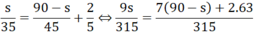
⇔ 9s = 7(90 - s) + 126
⇔ 9s = 756 - 7s
⇔ 16s = 756
⇔ s = 47,25(km)
Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là:
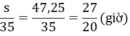
So sánh hai cách chọn ẩn, cách đầu tiên (chọn ẩn là thời gian từ lúc xe máy khởi hành đến lúc hai xe gặp nhau) cho cách giải ngắn gọn hơn vì phương trình đơn giản hơn.
9 tháng 2 2017
Ta thấy :
2a=a+a (1)
a^2=a.a (2)
Từ (1) và (2);ta có:
a.a > a+a
Nên a^2 > 2a