MN ơi giải giúp mk bài này vs: Cho tam giác ABC vuông tại A , \(BC=3\sqrt{5}\). Một hình vuông ADEF có cạnh AD=2 VÀ D thuộc AB, E thuộc BC, F thuộc AC. Biết AB>AC, và diện tích ADEF=\(\frac{4}{9}\)diện tích ABC, tính AB, AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2021
Vì DE // AC Theo hệ quảTa lét ta có : \(\frac{DB}{AB}=\frac{DE}{AC}\Rightarrow\frac{AB-AD}{AB}=\frac{DE}{AC}\)
\(\Rightarrow\frac{AB-2}{AB}=\frac{2}{AC}\Rightarrow AB.AC-2AC=2AB\)
\(\Rightarrow AB.AC-2\left(AC+AB\right)=0\)(*)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\)(**)
Từ (*) ; (**) ta có hệ : \(\hept{\begin{cases}AB.AC-2\left(AC+AB\right)=0\\AB^2+AC^2=45\end{cases}}\)
bấm casio nhé, mode 9 _ 1 _ ấn hệ ra _ ''=''
26 tháng 6 2021
Đặt \(\hept{\begin{cases}AB=x\\AC=y\end{cases}\left(x,y>0\right)}\)
Theo định lí Thales \(\frac{EF}{AB}=\frac{CF}{CA}\Rightarrow\frac{AB-EF}{AB}=\frac{CA-CF}{CA}\)
Hay \(\frac{x-2}{x}=\frac{2}{y}\Leftrightarrow xy=2\left(x+y\right)\left(1\right)\)
Theo định lí Pytagoras: \(AB^2+AC^2=BC^2\)hay \(x^2+y^2=45\left(2\right)\)
Từ (1),(2); ta có hệ phương trình: \(\hept{\begin{cases}xy=2\left(x+y\right)\\x^2+y^2=45\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\x^2+2xy+y^2-4\left(x+y\right)-45=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\\left(x+y\right)^2-4\left(x+y\right)-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=9\\x^2+y^2-45=0\end{cases}}\)(Vì x,y dương)
\(\Leftrightarrow\hept{\begin{cases}y=9-x\\x^2+\left(9-x\right)^2-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=9-x\\x=6\left(h\right)x=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\left(h\right)\hept{\begin{cases}x=3\\y=6\end{cases}}\)
Vậy \(AB=3,AC=6\) hoặc \(AB=6,AC=3.\)
20 tháng 3 2023
DE//AC
=>DE/AC=BE/BC
=>DE/8=BE/12
=>DE=2/3BE
EF//AB
=>EF/AB=CE/CB
=>CE/12=EF/6
=>EF=1/2CE
mà EF=DE
nên 2/3BE=1/2CE
mà BE+CE=12
nên BE=36/7cm; CE=48/7cm
=>DE=2/3*BE=2/3*36/7=72/21=24/7(cm)
5 tháng 8 2021
Bài 5:
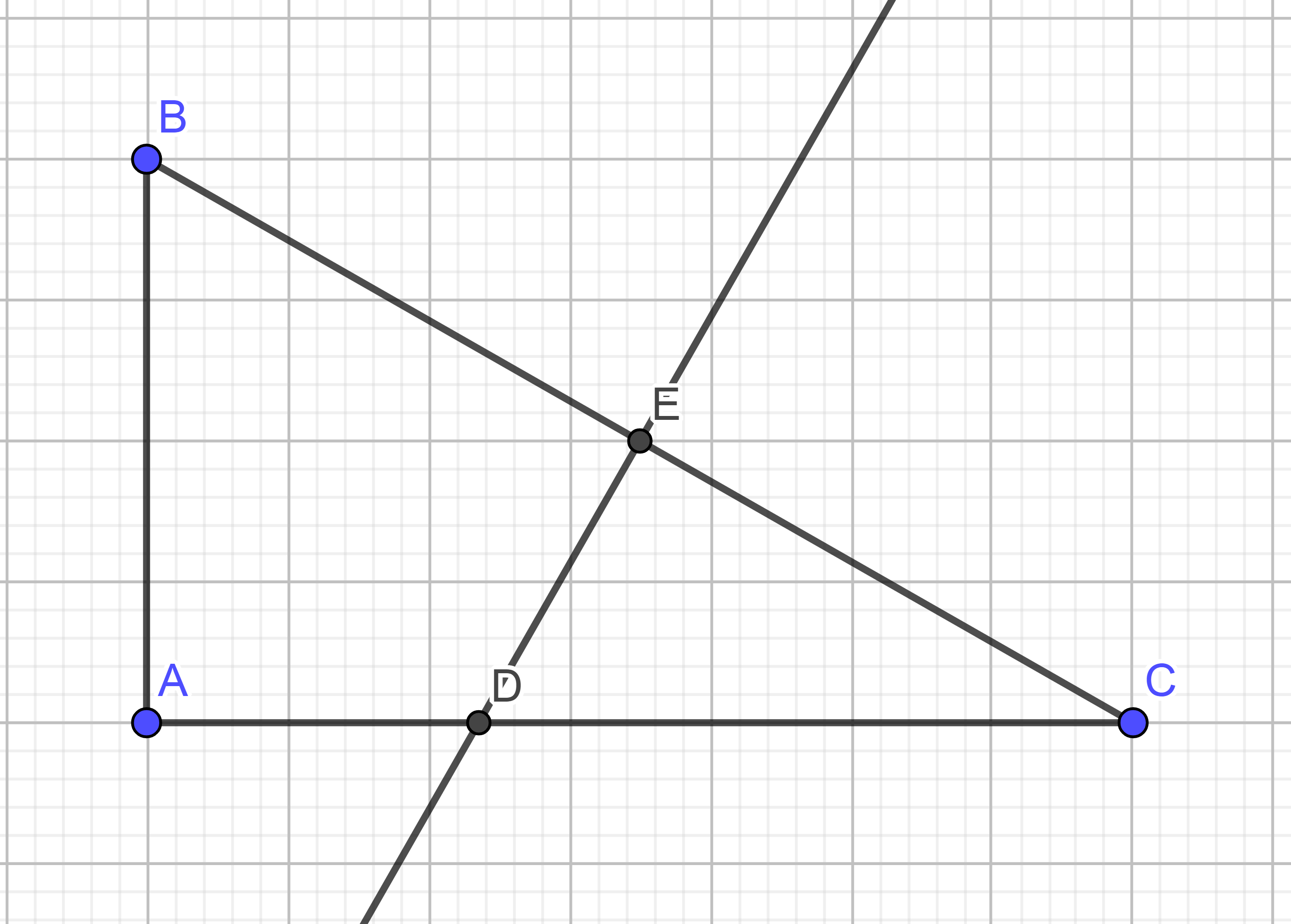
Xét ΔABC vuông tại A
Áp dụng Pytago ta có:
BC2 = AB2 + AC2
= 242 + 322
⇒ BC = 40
DE là trung trực của BC
⇒ E là trung điểm của BC; DE vuông góc với BC tại E
⇒ EC = BC/2 = 40/2 = 20
Xét ΔCED và ΔCAB có:
∠CED = ∠CAB = 90o
∠C chung
⇒ ΔCED đồng dạng ΔCAB
⇒ CE/CA = ED/AB
⇒ 12/32 = ED/24
⇒ ED = 9
31 tháng 10 2021
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật
Suy ra: AM=DE
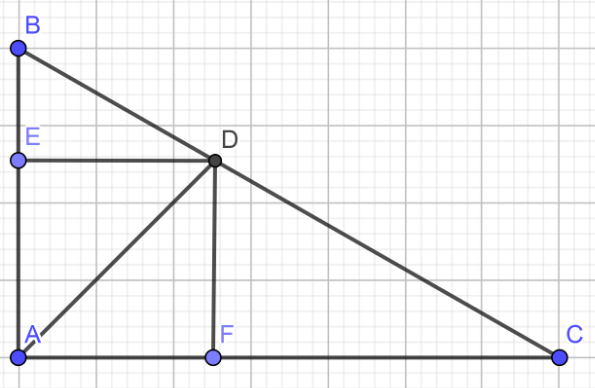
Kẻ đường cao AH của tam giác ABC. Ta có: SADEF = 2.2=4 => SABC = 9. Ta có :\(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.3\sqrt{5}.AH=9\Rightarrow AH=\frac{6}{\sqrt{5}}\).
Áp dụng ĐL Py-ta-go ta tính được \(AE=\sqrt{2^2+2^2}=2\sqrt{2}>\frac{6}{\sqrt{5}}\Rightarrow E\ne H\Rightarrow\)Tam giác AEH vuông tại H.
Ta có: \(\sin AEH=\frac{AH}{AE}=\frac{3}{\sqrt{10}}\Rightarrow AEH\approx71^034'\)=>Góc ECA = 180o-góc EAC-góc AEC = 180o - 45o - 71o34' = 63o26'
\(\Rightarrow\sin BCA=\sin63^026'=\frac{AB}{BC}\approx0,894\Rightarrow AB\approx6\left(cm\right)\). Vận dụng ĐL Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=3\)