Tìm ba số nguyên biết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
1 tháng 8 2023
Gọi 3 số lần lượt là n; n+1; n+2
3 tích lần lượt là:
\(n\left(n+1\right)=n^2+n\\ n\left(n+2\right)=n^2+2n\\ \left(n+1\right)\left(n+2\right)=n^2+3n+2\)
Theo đề bài, ta có:
\(n^2+n+n^2+2n+n^2+3n+2=242\\ \Leftrightarrow3n^2+6n-240=0\\ \Leftrightarrow3\left(n-8\right)\left(n+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}n=8\\n=-10\end{matrix}\right.\)
Vậy bộ 3 số đó là \(\left\{8;9;10\right\},\left\{-10;-9;-8\right\}\)
PA
12 tháng 9 2016
Gọi 3 số nguyên liến tiếp lần lượt là a ; a + 1 ; a + 2.
a(a + 1) + a(a + 2) + (a + 1)(a + 2) = 242
a2 + a + a2 + 2a + a2 + 3a + 2 = 242
3a2 + 6a + 2 = 242
3(a2 + 2a) = 242 - 2
a2 + 2a + 1 - 1 = 240 : 3
(a + 1)2 = 80 + 1
(a + 1)2 = 81
\(\left(a+1\right)^2=\left(\pm9\right)^2\)
\(a+1=\pm9\)
a + 1 = \(\pm9\)
a = \(\pm8\)
a + 2 = \(\pm10\)
Vậy 3 số nguyên đó là 8 ; 9 ; 10 hoặc - 8 ; - 9 ; - 10
12 tháng 9 2016
Gọi 3 số nguyên liên tiếp cần tìm là: a; a + 1; a + 2
Các tích lập được thỏa mãn là: a.(a + 1); (a + 1).(a + 2); (a + 2).a
Ta có: a.(a + 1) + (a + 1).(a + 2) + (a + 2).a = 242
=> a2 + a + (a + 1).a + (a + 1).2 + a2 + 2a = 242
=> a2 + a + a2 + a + 2a + 2 + a2 + 2a = 242
=> 3a2 + 6a + 2 = 242
=> 3a.(a + 2) = 242 - 2 = 240
=> a.(a + 2) = 240 : 3 = 80
=> a.(a + 2) = 8.10 = -10.(-8)
=> a = 8 hoặc a = -10
Vậy 3 số nguyên liên tiếp cần tìm là: 8; 9; 10 hoặc -10; -9; -8
TH
1
9 tháng 7 2015
ab+ba=10a+b+10b+a=11a+11b=11(a+b)
11(a+b) chia hết cho 11 mà ab+ba là số nguyên tố
=>a+b=1
=>ab=10
ab là hợp số nên không có số nguyên tố ab
OY
16 tháng 8 2021
1. Ta có: trong 25 số nguyên tố có 1 số nguyên tố chẵn còn lại là 24 số nguyên tố lẻ. Tổng của 24 số lẻ là một số chẵn nên tổng của 25 số nguyên tố nhỏ hơn 100 là số chẵn.
CM
14 tháng 5 2019
Đáp án là A
Ta có:
15 + (-3) + x = 23
12 + x = 23
x = 23 - 12
x = 11
TV
0
PT
1
TQ
5
D
24 tháng 4 2017
Chứng minh các số a; b; c nhất định phải là các số nguyên dương phân biệt
Ta có a.b.c = a+b+c
Giả sử a = b = c ta có a^3 = 3a => a^2 = 3. Ptrình này không cho nghiệm nguyên dương, nên a; b; c là 3 số nguyên dương phân biệt.
Tìm các số nguyên dương:
Giả sử a là số lớn nhất trong 3 số. Ta có a + b + c = a.b.c < 3a. Hay tích b.c <3. Vì a; b; c là các số nguyên dương; b.c <3. Do b;c nguyên dương nên tích b,c nguyên dương hay b.c = 1 hoặc b.c =2. Mặt khác chứng minh được b khác c nên b và c chỉ có thể là 1 và 2. Ở đây ta giả sử c là 1. thì b là 2. (b khác 2 thì tích b.c > 3 là vô lý).
Vậy ta có 1 + 2 + a = 1.2.a hay 3+a = 2a => a = 3.
Kết luận: Số cần tìm là 1; 2; 3 .
21 tháng 6 2017
Ra 5,4,1
Mình chỉ ra kết quả thôi, còn trình bày lằng nhằng lắm
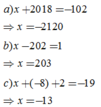
Ta có : \(\left(a+b-c\right)+\left(a-b+c\right)=-3+11\)
\(\Leftrightarrow2a=8\\ \Leftrightarrow a=4\)
\(\left(a-b+c\right)+\left(a-b-c\right)=11-1\)
\(\Leftrightarrow2a-2b=10\\ \Leftrightarrow2\cdot4-2b=10\\ \Leftrightarrow8-2b=10\\ \Leftrightarrow2b=8-10\\ \Leftrightarrow2b=-2\\ \Leftrightarrow b=-1\)
Thay a=4 b= -1 ta có :
\(4-1-c=-3\)
\(\Leftrightarrow3-c=-3\\ \Leftrightarrow c=6\)
Vậy \(a=4;b=-1;c=6\) là các giá trị cần tìm