hình thang ABCD(AB song song với CD) có AB=2cm, BD=4cm, CD=8cm. Chứng minh: góc A bằng góc DBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
0
TN
1
CM
20 tháng 12 2017
Ta có: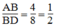 
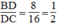
Suy ra: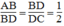 
Xét △ ABD và △ BDC, ta có:
∠ (ABD) = ∠ (BDC) (so le trong)
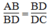(chứng minh trên)
Vây △ ABD đồng dạng △ BDC (c.g.c) ⇒ ∠ (BAD) = ∠ (DBC)
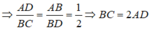
Tỉ số đồng dạng k = 1/2
Ta có: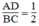 
, suy ra: BC = 2AD
24 tháng 3 2023
a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>AB/CD=OA/OC=OB/OD
=>5/CD=1/2
=>CD=10cm và OA*OD=OB*OC
b: Xét ΔOHA vuông tại H và ΔOKC vuông tại K có
góc AOH=góc KOC
=>ΔOHA đồng dạng với ΔOKC
=>OH/OK=OA/OC=1/2
c: AE/AD+CF/BC
=AE/AD+1-BF/BC
=1
19 tháng 8 2023
Xét ΔABD và ΔBDC có
AB/BD=BD/DC
góc ABD=góc BDC
=>ΔABD=ΔBDC
=>góc BAD=góc DBC
CM
14 tháng 5 2019
. a) HS tự chứng minh
b) Kẻ đường cao AH, BK,chứng minh được DH = CK
Ta được H D = C D − A B 2 = 3 c m
Þ AH = 4cm Þ SABCD = 20cm2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 7 2023
Bài 5
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
20 tháng 7 2023
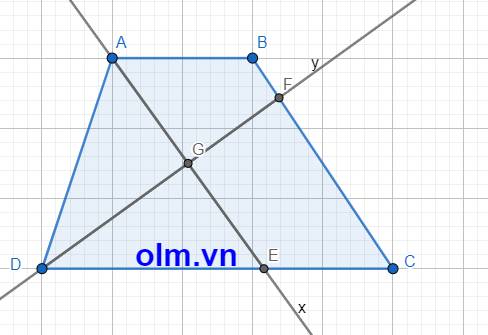
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)
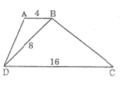
bạn tự vẽ hình nha
Xét \(\Delta\)ABD và \(\Delta\)BDC có:
góc ABD=góc BDC(vì AB//CD)
\(\dfrac{AB}{DB}=\dfrac{BD}{DC}=\dfrac{1}{2}\)
\(\Rightarrow\)\(\Delta\)ABD đồng dạng \(\Delta\)BDC(c.g.c)
\(\Rightarrow\)góc A=góc DBC