Chứng minh các bất đẳng thức sau :
a) \(\tan x>\sin x;0< x< \dfrac{\pi}{2}\)
b) \(1+\dfrac{1}{2}x-\dfrac{x^2}{8}< \sqrt{1+x}< 1+\dfrac{1}{2}x\) với \(0< x< +\infty\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
31 tháng 3 2021
\(tan^2x-sin^2x=tan^2x.sin^2x\)
\(\Leftrightarrow\dfrac{sin^2x}{cos^2x}-sin^2x=\dfrac{sin^2x}{cos^2x}.sin^2x\)
\(\Leftrightarrow\dfrac{sin^2x\left(1-cos^2x\right)}{cos^2x}=\dfrac{sin^4x}{cos^2x}\)
\(\Leftrightarrow\dfrac{sin^2x.sin^2x}{cos^2x}=\dfrac{sin^4x}{cos^2x}\)
\(\Rightarrowđpcm\)
23 tháng 3 2022
\(a)sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)(luôn đúng)
17 tháng 5 2021
a) Ta có: \(1-\frac{\sin^2x}{1+\cot x}-\frac{\cos^2x}{1+\tan x}=1-\frac{\sin^2x}{1+\frac{\cos x}{\sin x}}-\frac{\cos^2x}{1+\frac{\sin x}{\cos x}}\) (Đk: sinx và cosx khác 0)
\(=1-\frac{\sin^3x}{\sin x+\cos x}-\frac{\cos^3x}{\cos x+\sin x}\)
\(=1-\frac{\left(\sin x+\cos x\right)\left(\sin^2x-\sin x.\cos x+\cos^2x\right)}{\sin x+\cos x}\)
\(=1-\left(\sin^2x+\cos^2x-\sin x.\cos x\right)\) (do sinx + cosx luôn khác 0)
\(=\sin x.\cos x\) ( do \(\sin^2x+\cos^2x=1\))
b) Ta có: \(\frac{\sin^2x+2\cos x-1}{2+\cos x-\cos^2x}=\frac{\left(\sin^2x-1\right)+2\cos x}{-\left(\cos x+1\right)\left(\cos x-2\right)}\) (Đk: cosx khác -1 và 2)
\(=\frac{-\cos x\left(\cos x-2\right)}{-\left(\cos x+1\right)\left(\cos x-2\right)}\)
\(=\frac{\cos x}{1+\cos x}\)
19 tháng 5 2021
a) Ta có: 1−sin2x1+cotx −cos2x1+tanx =1−sin2x1+cosxsinx −cos2x1+sinxcosx (Đk: sinx và cosx khác 0)
=1−sin3xsinx+cosx −cos3xcosx+sinx
=1−(sinx+cosx)(sin2x−sinx.cosx+cos2x)sinx+cosx
=1−(sin2x+cos2x−sinx.cosx) (do sinx + cosx luôn khác 0)
=sinx.cosx ( do sin2x+cos2x=1)
b) Ta có: sin2x+2cosx−12+cosx−cos2x =(sin2x−1)+2cosx−(cosx+1)(cosx−2) (Đk: cosx khác -1 và 2)
=−cosx(cosx−2)−(cosx+1)(cosx−2)
=cosx1+cosx
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2020
\(\frac{sinx+cosx-1}{1-cosx}=\frac{\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{sin^2x-\left(cosx-1\right)^2}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{sin^2x-cos^2x+2cosx-1}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{1-cos^2x-cos^2x+2cosx-1}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{2cosx-2cos^2x}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{2cosx\left(1-cosx\right)}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{2cosx}{sinx-cosx+1}\)
MT
Chứng minh đẳng thức:
\(\frac{\sin^2x}{\sin x-\cos x}-\frac{\sin x+\cos x}{\tan^2x-1}=\sin x+\cos x\)
2
9 tháng 4 2017
\(\frac{\sin^2x}{\sin x-\cos x}-\frac{\sin x+\cos x}{\tan^2x-1}\)
\(=\frac{\sin^2x}{\sin x-\cos x}-\frac{\sin x+\cos x}{\frac{\sin^2x-\cos^2x}{\cos^2x}}\)
\(=\frac{\sin^2x}{\sin x-\cos x}-\frac{\cos^2x}{\sin x-\cos x}=\sin x+\cos x\)
Xong
CM
19 tháng 12 2019
iểm tra với n = 1
Giả sử đã có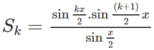 
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
DT
1
7 tháng 8 2017
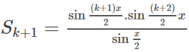
\(tan^2x-sin^2x=\frac{sin^2x}{cos^2x}-sin^2x\)
\(=sin^2x.\left(\frac{1}{cos^2x}-1\right)=sin^2x.\frac{sin^2x}{cos^2x}=tan^2x.sin^2x\)
HN
1 tháng 4 2017
a/ \(\dfrac{\sin x+\cos x-1}{1-\cos x}=\dfrac{2\cos x}{\sin x-\cos x+1}\)
\(\Leftrightarrow-2\cos^2x+2\cos x-2\cos x+2\cos^2x=0\)
\(\Leftrightarrow0=0\) (đúng)
\(\RightarrowĐPCM\)
HN
1 tháng 4 2017
b/ \(\tan a.\tan b=\dfrac{\tan a+\tan b}{\cot a+\cot b}\)
\(\Leftrightarrow\tan a.\tan b.\left(\cot a+\cot b\right)=\tan a+\tan b\)
\(\Leftrightarrow\tan a.\tan b.\cot a+\tan a.\tan b.\cot b=\tan a+\tan b\)
\(\Leftrightarrow\tan b+\tan a=\tan a+\tan b\) (đúng)
\(\RightarrowĐPCM\)
17 tháng 8 2023
a: \(2\cdot cot\left(\dfrac{pi}{2}-x\right)+tan\left(pi-x\right)\)
\(=2\cdot tanx-tanx\)
=tan x
b: \(sin\left(\dfrac{5}{2}pi-x\right)+cos\left(13pi+x\right)-sin\left(x-5pi\right)\)
\(=sin\left(\dfrac{pi}{2}-x\right)+cos\left(pi+x\right)+sin\left(pi-x\right)\)
\(=cosx-cosx+sinx=sinx\)
g'(x) là đạo hàm của g(x) phải không bạn? Xét đạo hàm tới 2 lần lận à?