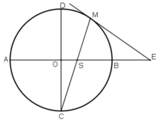
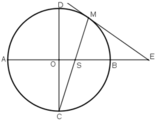
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES = EM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
11 tháng 4 2017
Ta có \(\widehat{MSE}\) = 
(1)
( vì \(\widehat{MSE}\) là góc có đỉnh S ở trong đường tròn (O))
\(\widehat{CME}\) = 
= 
(2)
(\(\widehat{CME}\) là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết 
= 
(3)
Từ (1), (2), (3) ta có: \(\widehat{MSE}\)= \(\widehat{CME}\)từ đó \(\Delta\)ESM là tam giác cân và ES = EM
CM
3 tháng 12 2018
+ M S E ^ là góc có đỉnh S ở trong đường tròn (O)
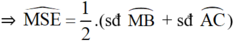
+ E S M ^ là góc tạo bởi tiếp tuyến ME và đây MC
⇒ E M S ^ = 1 2 . s đ M C ⏜ = 1 2 . s đ M B ⏜ + s đ B C ⏜
CM
5 tháng 12 2019
Kiến thức áp dụng
+ Số đo của góc có đỉnh bên trong đường tròn bằng một nửa tổng số đo của hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng một nửa số đo của cung bị chắn.
3 tháng 2 2016
bạn vẽ hình ra __________nhìn hình nha!
Vì AB và CD là 2 đường kính vuông góc với nha(gt)
nên chia đường tròn thành 4 cung = nhau
cung AC= cung CB
Có góc BSM=1/2(sđ c.AC + sđ c.BM) (vì góc có đỉnh ở bên trong đường tròn)
<=>g.BSM = 1/2 (sđc.CB +sđc.BM) (vì c.AC=c.BD)
<=>g.BSM =1/2 sđc.CM (1)
Lại có g.CME = 1/2 sđ c.CM (góc tạo bởi 1 tia tiếp tuyến và 1 dây cung) (2)
Từ (1) và (2) => g.BSM =g.CME
=> tam giác EMS cân tại E
=> SE=EM
Ta có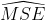
= 
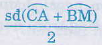(1)
( vì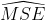
là góc có đỉnh S ở trong đường tròn (O))
(
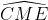là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết
= 
(3)
Từ (1), (2), (3) ta có: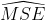
= 
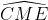từ đó ∆ESM là tam giác cân và ES = EM
Bạn ơi nếu đề cũng như vậy nhưng họ bắt mình chứng minh tứ giác OMDS nội tiếp thì phải làm sao ạ ?