Cho hai đường thẳng AB và CD cắt nhau tại O .Tìm tập hợp các điểm cách đều 2 đường thẳng AB và CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.
1
CM
5 tháng 11 2017
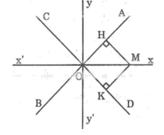
* Xét điểm M nằm trong góc AOD
Kẻ MH ⊥ OA, MK ⊥ OD
Xét hai tam giác MHO và MKO:
∠(MHO) = ∠(MKO) = 90o
MH = MK
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO
(cạnh huyền - cạnh góc vuông)
Suy ra: ∠(MOH) = ∠(MOK)(2 góc tương ứng)
Hay OM là tia phân giác của ∠(AOD).
* Ngược lại, M nằm trên tia phân giác của ∠(AOD)
Xét hai tam giác vuông MHO và MKO, ta có:
∠(MHO) = ∠(MKO)= 90o
∠(MOH) = ∠(MOK)
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO (cạnh huyền - góc nhọn)
Suy ra: MH = MK (2 cạnh tương ứng)
Vậy tập hợp các điểm M cách đều OA và OD là tia phân giác Ox của góc AOD.
Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
DT
cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.
0
18 tháng 5 2022
Nếu điểm M nằm trong góc AOD thì kẻ MH vuông góc với OA, MK vuông góc với OD
Xét ΔMHO vuông tại H và ΔMKO vuông tại K có
MO chung
MH=MK
Do đó: ΔMHO=ΔMKO
Suy ra: \(\widehat{MOH}=\widehat{MOK}\)
=>M nằm trên tia phân giác của góc AOD
Vì ΔMHO=ΔMKO nên MH=MK
=>Tập hợp điểm M cách đều OA và OD là phân giác Ox của góc AOD
Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
ND
2
23 tháng 3 2018
tập hợp các điểm cách đều 2 đường thẳng AB và CD
chỉ được 1 điểm
điểm giao điểm với 2 đt đó là O
HK
0
BR
1
17 tháng 4 2018
các điểm cách đêu đoạn thẳng AB và CD là điểm nằm trên tia phân giác của góc AOD,AOC,BOD,BOC
bằng 110º. Tính ba góc còn lại
– 
, 
, 
.
< 
)
, 
30 tháng 8 2015
Bài của bạn hay, nhưng bạn viết phần 2/ ẩu quá!.
Câu 1. Vì O là tâm đường tròn qua hai điểm A,B nên \(OA=OB\to O\) nằm trên trung trực của đoạn thẳng AB cố định. Đảo lại với mỗi điểm O nằm trên trung trực AB, ta vẽ đường tròn tâm O bán kính OA thì đường tròn này đi qua AB.
Câu 2. Vì IJ là đường kính của đường tròn (O) nên \(JM\perp CI,IN\perp CJ,CE\perp JI\) do đó ba đường thẳng \(JM,CE,IN\) là ba đường cao của tam giác \(CJI\to\) ba đường này đồng quy tại trực tâm tam giác \(CJI.\) Vậy \(D\) nằm trên đường thẳng AB.
Gọi F là giao điểm của tiếp tuyến tại M với đường thẳng AB. T
a có \(\angle FMC=90^{\circ}-\angle OMI=90^{\circ}-\angle OIM=\angle ECI=\angle MCF\to\Delta FMC\) cân ở F. Mà tam giác MCD vuông ở M nên \(\angle FMD=\angle FDM\to\Delta DFM\) cân ở F. Thành thử \(F\) là trung điểm CD. Vậy tiếp tuyến ở M cắt CD tại trung điểm của CD. Tương tự chứng minh được tiếp tuyến tại N của (O) cũng đi qua trung điểm của CD. Vậy hai tiếp tuyến tại M,N cắt nhau ở tại trung điểm CD.