Cho 5 đoạn thẳng với các độ dài 3, 5, 7, 9, 11. Chọn ngẫu nhiên ra ba đoạn thẳng.
a) Mô tả không gian mẫu
b) Xác định biến cố A : "Ba đoạn thẳng chọn ra thành một tam giác" và tính xác suất của A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
18 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
4 tháng 2 2017
a) Ω gồm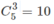 
bộ ba đoạn thẳng khác nhau trong số năm đoạn thẳng đã cho.
b) A gồm các bộ có tổng của hai số lớn hơn số còn lại.
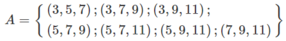
Ta có n(A) = 7
Vậy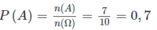 
CM
8 tháng 2 2019
Chọn D
Lấy ba đoạn thẳng từ năm đoạn thẳng có
C
5
3
= 10 cách. Suy ra số phần tử của không gian mẫu là 
Gọi A là biến cố: " Ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác ".
Khi đó 3 đoạn thẳng được chọn thỏa mãn tính chất: Tổng độ dài 2 đoạn thẳng luôn lớn hơn độ dài đoạn thẳng còn lại.
Có 3 bộ thỏa mãn là 
Vậy xác suất để ba đoạn thẳng lấy ra tạo thành ba cạnh của một tam giác là
CM
5 tháng 8 2018
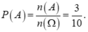
Biến cố A : "ba điểm tạo thành tam giác", tức là ba điểm không thẳng hàng.
Có 2 trường hợp:
- Hai điểm thuộc a và một điểm thuộc b có C 6 2 . C 5 1 cách
- Hai điểm thuộc b và một điểm thuộc a có C 6 1 . C 5 2 cách
Suy ra,số phần tử của biến cố A là:
Ω A = C 6 2 . C 5 1 + C 6 1 . C 5 2 = 135
Đáp án A.
