Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Tìm xác suất sao cho trong hai người đó :
a) Cả hai đều là nữ
b) Không có nữ nào
c) Ít nhất một người là nữ
d) Có đúng một người là nữ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
18 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
10 tháng 5 2019
Số cách chọn là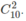 
. Kí hiệu
A
k
là biến cố: "Trong hai ngườiđã chọn, có đúng k nữ", k = 0, 1, 2
a) Cần tính P ( A 2 ) .
Ta có:
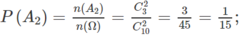
b) Tương tự
CM
26 tháng 1 2019
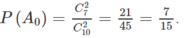
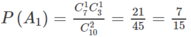
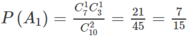
Chọn B.
Phương pháp
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A, n Ω là số phấn tử
của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu n Ω = C 20 2
Gọi A là biến cố “Hai người được chọn có it nhất một nữ” thì A là biến cố hai người được chọn không có nữ nào, tức là ta chọn 2 người trong số 7 nam.
Khi đó n A = C 7 2 ⇒ n A = C 10 2 - C 7 2
Xác suất để hai người được chọn có it nhất một nữ là P = C 10 2 - C 7 2 C 10 2 = 8 15
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Số cách chọn 2 bạn bất kì trong 10 bạn đó là \(C_{10}^2\)
Cách 1:
Trường hợp 1: Hai bạn được chọn gồm 1 nam và 1 nữ
Có 7 cách chọn một bạn nam
Có 3 cách chọn một bạn nữ
=> Có 3.7 =21 cách chọn
Trường hợp 2: Hai bạn được chọn đều là nữ
Số cách chọn 2 trong 3 bạn nữ là: \(C_3^2\)
=> Xác suất để trong hai người được chọn có ít nhất một nữ là: \(\frac{{21 + C_3^2}}{{C_{10}^2}} = \frac{8}{{15}}\)
Chọn B.
Cách 2:
Gọi A là biến cố: “trong hai người được chọn có ít nhất một nữ”
Biến cố đối \(\overline A \): “trong hai người được không có bạn nữ nào” hay “hai người được chọn đều là nam”
Ta có: Số cách chọn 2 trong 7 bạn nam là \(n(\overline A ) = C_7^2\)
\(\begin{array}{l} \Rightarrow P(\overline A ) = \frac{{C_7^2}}{{C_{10}^2}} = \frac{{21}}{{45}} = \frac{7}{{15}}\\ \Rightarrow P(A) = 1 - P(\overline A ) = 1 - \frac{7}{{15}} = \frac{8}{{15}}\end{array}\)
Chọn B.
CM
26 tháng 3 2019
Đáp án A
Không gian mẫu là “Chọn ngẫu nhiên 2 người từ 10 học sinh trong tổ đó”. Suy ra số phần tử trong không gian mẫu là n ( Ω ) = C 10 2
Gọi A là biến cố “2 người được chọn là nữ” thì kết quả thuận lợi cho biến cố A là n ( A ) = C 3 2
Vậy xác suất cần tính là P ( A ) = n ( A ) n ( Ω ) = C 3 2 C 10 2 = 1 15 .
