Lập phương trình ba đường trung trực của một tam giác có trung điểm các cạnh lần lượt là \(M\left(-1;0\right);N\left(4;1\right);P\left(2;4\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2021
Đường thẳng AB nhận \(\overrightarrow{n}=\left(1;2\right)\) làm vecto pháp tuyến
AB đi qua A (1; -1) nên nó có phương trình là
x - 1 + 2 (y + 1) = 0 hay x + 2y + 1 = 0
Gọi M là trung điểm của AB ⇒ M ∈ Δ, tọa độ của M có dạng
M (t ; 2t + 1) với t là số thực và \(\overrightarrow{AM}=\left(t-1;2t+2\right)\)
⇒ AM ⊥ Δ
⇒ \(\overrightarrow{AM}.\overrightarrow{n}=0\)
⇒ t + 1 + 2. (2t + 2) = 0
⇒ t = -1
Vậy M (- 1; - 1)
M là trung điểm của AB => Tọa độ B
Làm tương tự như thế sẽ suy ra tọa độ C
25 tháng 2 2023
Theo đề, ta có:
xB+xC=-2 và xA+xC=2 và xA+xB=18
=>xA=11; xB=7; xC=-9
Theo đề, ta có:
yB+yC=-2 và yC+yA=18 và yA+yB=2
=>yA=11; yB=-9; yC=7
=>A(11;11); B(7;-9); C(-9;7)
*PTTQ của AB
vecto AB=(-4;-20)=(1;5)
=>VTPT là (-5;1)
PT của AB là -5(x-7)+1(y+9)=0
=>-5x+35+y+9=0
=>-5x+y+44=0
*PT của AC
vecto AC=(-20;-4)=(5;1)
=>VTPT là (-1;5)
PT của AC là -1(x+9)+5(y-7)=0
=>-x-9+5y-35=0
=>-x+5y-44=0
*PT của BC
vecto BC=(-16;16)=(-1;1)
=>VTPT là (1;1)
Phương trình BC là:
1(x+9)+1(y-7)=0
=>x+y+2=0
15 tháng 1
M là trung điểm của BC
=>\(\left\{{}\begin{matrix}x_B+x_C=2\cdot x_M=2\cdot2=4\\y_B+y_C=2\cdot y_M=2\cdot3=6\end{matrix}\right.\)(1)
N là trung điểm của AC
=>\(\left\{{}\begin{matrix}x_A+x_C=2\cdot x_N=2\cdot4=8\\y_A+y_C=2\cdot y_N=2\cdot\left(-1\right)=-2\end{matrix}\right.\left(2\right)\)
P là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot x_P=2\cdot\left(-3\right)=-6\\y_A+y_B=2\cdot y_P=2\cdot5=10\end{matrix}\right.\)(3)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_B+x_C=4\\x_A+x_C=8\\x_A+x_B=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=4-x_C\\x_A=8-x_C\\4-x_C+8-x_C=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12-2x_C=-6\\x_B=4-x_C\\x_A=8-x_C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=9\\x_B=4-9=-5\\x_A=8-9=-1\end{matrix}\right.\)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}y_B+y_C=6\\y_A+y_C=-2\\y_A+y_B=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_B=6-y_C\\y_A=-2-y_C\\6-y_C-2-y_C=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4-2\cdot y_C=10\\y_B=6-y_C\\y_A=-2-y_C\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_C=-3\\y_B=6+3=9\\y_A=-2+3=1\end{matrix}\right.\)
Vậy: C(9;-3); B(-5;9); A(-1;1)
Gọi (d1): ax+by+c=0 là phương trình đường thẳng AB
A(-1;1); B(-5;9)
\(\overrightarrow{AB}=\left(-4;8\right)=\left(-1;2\right)\)
=>VTPT là (2;1)
Phương trình AB là:
2[x-(-1)]+1(y-1)=0
=>2(x+1)+1(y-1)=0
=>2x+2+y-1=0
=>2x+y+1=0
Gọi (d2): ax+by+c=0 là phương trình đường thẳng AC
A(-1;1); C(9;-3)
\(\overrightarrow{AC}=\left(10;-4\right)=\left(5;-2\right)\)
=>VTPT là (2;5)
Phương trình AC là:
2(x+1)+5(y-1)=0
=>2x+2+5y-5=0
=>2x+5y-3=0
Gọi (d3): ax+by+c=0 là phương trình đường thẳng BC
B(-5;9); C(9;-3)
\(\overrightarrow{BC}=\left(14;-12\right)=\left(7;-6\right)\)
=>VTPT là (6;7)
Phương trình đường thẳng CB là:
6(x+5)+7(y-9)=0
=>6x+30+7y-63=0
=>6x+7y-33=0
\(\overrightarrow{BC}=\left(7;-6\right)\)
=>VTPT là (6;7)
mà trung điểm của BC là M(2;3)
nên Phương trình đường trung trực của BC là:
\(6\left(x-2\right)+7\left(y-3\right)=0\)
=>6x-12+7y-21=0
=>6x+7y-33=0
C(9;-3); B(-5;9); A(-1;1)
\(\overrightarrow{AC}=\left(10;-4\right)=\left(5;-2\right)\)
=>VTPT là (2;5)
Phương trình đường trung trực của AC là:
\(2\left(x-4\right)+5\left(y+1\right)=0\)
=>2x-8+5y+5=0
=>2x+5y-3=0
\(\overrightarrow{AB}=\left(-4;8\right)=\left(-1;2\right)\)
=>VTPT là (2;1)
Phương trình trung trực của AB là:
\(2\left(x+3\right)+1\left(y-5\right)=0\)
=>2x+6+y-5=0
=>2x+y+1=0
17 tháng 9 2023
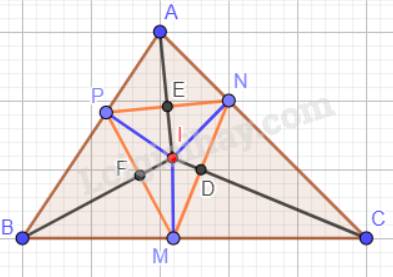
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
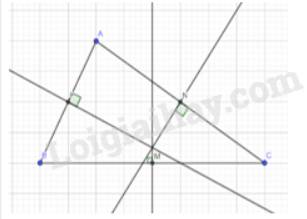
gọi \(\Delta_1,\Delta_2,\Delta_3\) lần lược là các đường trung trực đi qua M,N,P.
ta có : \(\overrightarrow{n}_{\Delta_1}=\overrightarrow{NP}=\left(-2;3\right).\)
vậy \(\Delta_1\) có phương trình \(-2\left(x+1\right)+3y=0\Leftrightarrow2x-3y+2=0\)
ta có : \(\overrightarrow{n}_{\Delta_2}=\overrightarrow{MP}=\left(3;4\right).\)
vậy \(\Delta_2\) có phương trình \(3\left(x-4\right)+4\left(y-1\right)=0\Leftrightarrow3x+4y-16=0\)
ta có : \(\overrightarrow{n}_{\Delta_3}=\overrightarrow{MN}=\left(5;1\right).\)
vậy \(\Delta_3\) có phương trình \(5\left(x-2\right)+\left(y-4\right)=0\Leftrightarrow5x+y-14=0\)