Cho hình bình hành ABCD (AB<AD).Tia phân giác góc A cắt BC tại I,tia phân giác C^ cắt AD tại K.
a)So sánh hai góc IAD^ và CKD^
b)Tứ giác AICK LÀ hình gì ? Giải thích
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình

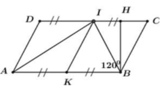
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A

Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)

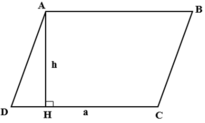
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

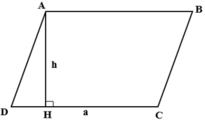
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

a) Cạnh đáy AB là: 9 x 2 =18(cm)
Cạnh bên BC là: 18 - 3 = 15(cm)
Diện tích hình bình hành ABCD là: 18 x 9 = 162(cm2)
b) Chu vi hình bình hành ABCD là: (18 + 15) x 2 = 66(cm)
Đ/S: a) 162 cm2
b) 66 cm
a: Ta có: \(\widehat{IAD}=\dfrac{\widehat{DAB}}{2}\)
\(\widehat{BCK}=\dfrac{\widehat{BCD}}{2}\)
mà \(\widehat{DAB}=\widehat{BCD}\)
nên \(\widehat{IAD}=\widehat{BCK}\)
mà \(\widehat{BCK}=\widehat{DKC}\)
nên \(\widehat{IAD}=\widehat{CKD}\)
b: Ta có: \(\widehat{IAD}=\widehat{CKD}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên AI//KC
Xét tứ giác AICK có
AI//KC
AK//IC
Do đó: AICK là hình bình hành