Dùng định nghĩa, tìm các giới hạn sau :
a) \(\lim\limits_{x\rightarrow4}\dfrac{x+1}{3x-2}\)
b) \(\lim\limits_{x\rightarrow+\infty}\dfrac{2-5x^2}{x^2+3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2023
a: \(=lim_{x->-\infty}\dfrac{2x-5+\dfrac{1}{x^2}}{7-\dfrac{1}{x}+\dfrac{4}{x^2}}\)
\(=\dfrac{2x-5}{7}\)
\(=\dfrac{2}{7}x-\dfrac{5}{7}\)
\(=-\infty\)
b: \(=lim_{x->+\infty}x\sqrt{\dfrac{1+\dfrac{1}{x}+\dfrac{3}{x^2}}{3x^2+4-\dfrac{5}{x^2}}}\)
\(=lim_{x->+\infty}x\sqrt{\dfrac{1}{3x^2+4}}=+\infty\)
2
18 tháng 11 2023
`a)lim_{x->+oo}[x+1]/[x^2+x+1]`
`=lim_{x->+oo}[1/x+1/[x^2]]/[1+1/x+1/[x^2]]`
`=0`
`b)lim_{x->+oo}[3x+1]/[3x^2-x+5]`
`=lim_{x->+oo}[3/x+1/[x^2]]/[3-1/x+5/[x^2]]`
`=0`
`c)lim_{x->-oo}[3x+5]/[\sqrt{x^2+x}]`
`=lim_{x->-oo}[3+5/x]/[-\sqrt{1+1/x}]`
`=-3`
`d)lim_{x->+oo}[-5x+1]/[\sqrt{3x^2+1}]`
`=lim_{x->+oo}[-5+1/x]/[\sqrt{3+1/[x^2]}]`
`=-5/3`
HT
9 tháng 2 2021
a/ \(=\lim\limits_{x\rightarrow4^-}\dfrac{5-2x}{4-x}=\dfrac{-3}{0}=-\infty\)
b/ \(=\lim\limits_{x\rightarrow+\infty}x^3\left(-1+\dfrac{1}{x}-\dfrac{2}{x^2}+\dfrac{1}{x^3}\right)=-\infty\)
HT
9 tháng 2 2021
a/ \(=\lim\limits_{x\rightarrow4^-}\dfrac{5-2x}{4-x}=-\infty\)
b/ \(=\lim\limits_{x\rightarrow+\infty}x^3\left(-1\right)=-\infty\)
a) Hàm số f(x) =
xác định trên R\{
} và ta có x = 4 ∈ (
;+∞).
Giả sử (xn) là dãy số bất kì và xn ∈ (
;+∞); xn ≠ 4 và xn → 4 khi n → +∞.
Ta có lim f(xn) = lim
= 
= 
.
Vậy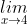
= 
.
b) Hàm số f(x) =
xác định trên R.
Giả sử (xn) là dãy số bất kì và xn → +∞ khi n → +∞.
Ta có lim f(xn) = lim
= lim 
= -5.
Vậy
= -5.