Viết phương trình của dao động điều hòa và giải thích các đại lượng trong phương trình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình của dao động điều hòa x= Acos(ωt + φ)
Trong đó :
- x : li độ của dao động (độ lệch của vật khỏi vị trí cân bằng) có đơn vị là centimet hoặc mét (cm ; m)
- A : biên độ dao động, có đơn vị là centimet hoặc mét (cm ; m)
- ω : tần số góc của dao động có đơn vị là radian trên giây (rad/s)
- (ωt + φ) : pha của dao động tại thời điểm t, có đơn vị là radian (rad)
- φ: pha ban đầu của dao động, có đơn vị là radian (rad)

Ta có: `x=Acos(\omega t+\pi/2)`
`=>` Để vẽ đồ thị hoặc viết phương trình của một dao động điều hòa cần những đại lượng vật lí là:
+, `A` là biên độ dao động `(m;cm;mm;....)`
+, `\omega` là tần số góc của dao động `(rad//s)`
+, `\varphi` là pha ban đầu của dao động `(rad)`.

Đáp án B
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x; x1; x2: 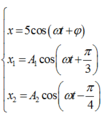
Suy ra :
+ Độ lệch pha giữa x và x1 là :![]()
+ Độ lệch pha giữa x và x2 là : 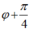
+ Độ lệch pha giữa x1 và x2 là : 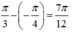
=> Ta có giản đồ vecto :
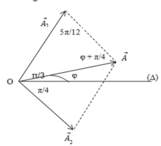
- Áp dụng định lí hàm số sin trong tam giác ta có:
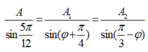
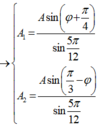
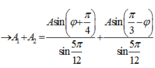
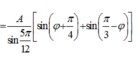
có: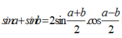
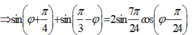
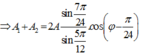
Để [A1 + A2] đạt cực đại thì 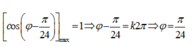

+ Các đại lượng A, ω và φ là hằng số (A và ω luôn dương)
+ từ đề thấy x phụ thuộc vào t theo dạng hàm số cos => Chọn D.


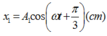
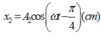
Phương tridnh dao động điều hòa là x = Acos(ωt+ Ø), trong đó:
- x là li độ của dao động
- A là biên độ dao động
- ω là tần số góc của đơn vị, có đơn vị là rad/s
- (ωt+ Ø) là pha của dao động tại thời điểm t, có đơn vị là rad,
- Ø là pha ban đầu của dao động
Phương trình dao động điều hòa
x=Acos(\(\omega\)t + \(\varphi\))
Trong đó x là li độ,
A là biên độ,
(\(\omega\)t + \(\varphi\)) là pha dao động (thường dùng đơn vị rad),
\(\varphi\) là pha ban đầu,
\(\omega\) là tần số góc (thường dùng đơn vị rad/s).