Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \) là góc CBD và số đo \(\widehat {CBD} = {30^o}\).
Góc giữa hai vectơ \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) là góc ADB.
Ta có: \(\widehat {ACB} = \widehat {CBD} + \widehat {CDB}\) (tính chất góc ngoài)
\(\begin{array}{l} \Leftrightarrow \widehat {CDB} = {80^o} - {30^o} = {50^o}\\ \Leftrightarrow \widehat {ADB} = {50^o}\end{array}\)
Vậy số đo góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) lần lượt là \({30^o},{50^o}\)
bài này ez mà :D ( Tự vẽ hình ) Vì EF // AB nên ta có thể viết như sau:
\(\overrightarrow{AB}.\overrightarrow{EG}=\overrightarrow{EF}.\overrightarrow{EG}=\overrightarrow{EF}\left(\overrightarrow{EF}+\overrightarrow{FG}\right)=EF^2+\overrightarrow{EF}.\overrightarrow{FG}=a^2\)
( Vì: \(\overrightarrow{EF}.\overrightarrow{FG}=\left|\overrightarrow{EF}\right|.\left|\overrightarrow{FG}\right|.\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=0\)) ( \(\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=90^0=0\))
Ta có. EG//AC (do ACGE là hình chữ nhật)
⇒ A B , E G = A B , A C = B A C = 45 o
Đáp án cần chọn là C
Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
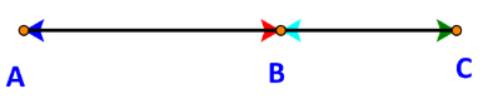
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.
a) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
b) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
