Question

[Đinh Thị Ngọc Anh]

Cho \(\Delta ABC,\widehat{A}=120^O\). Các tia phân giác của góc A và góc C cắt nhau ở O, cắt các cạnh BC và AC lần lượt ở D vả E. Đường phân giác của góc ngoài đỉnh B của tam giác ABC cắt đường thẳng AC tại F.Chứng minh:

a) \(BO\perp BF\)

b) \(\widehat{BDF}=\widehat{ADF}\)

c) Ba điểm D,E,F thẳng hàng

Answer 1

[Hồ Quốc Đạt]

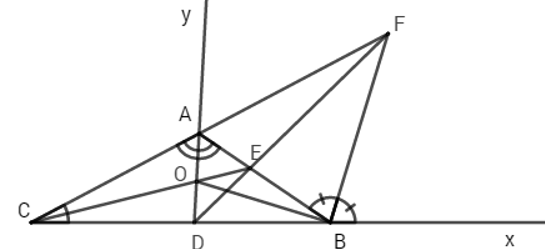
a, Ta có:

Trong \(\Delta ABC\) có AD là phân giác của \(\widehat{BAC}\)

CE là phân giác của \(\widehat{ACB}\)

\(\Rightarrow\) BO là phân giác \(\widehat{BAC}\)

\(\Rightarrow\widehat{B_1}=\widehat{B_2}\)

Ta có: BF là phân giác của \(\widehat{ABx}\)

\(\Rightarrow\widehat{B_3}=\widehat{B_4}\)

Có: \(\widehat{B_1}+\widehat{B_2}+\widehat{B_3}+\widehat{B_4}=180^0\)(\(\widehat{xBC}\) là góc bẹt)

Hay \(\widehat{B_1}+\widehat{B_1}+\widehat{B_3}+\widehat{B_3}=180^0\)

\(\Rightarrow\widehat{2B_1}+\widehat{2B_3}=180^0\)

\(\Rightarrow2.\left(\widehat{B_1}+\widehat{B_3}\right)=180^0\)

\(\Rightarrow\widehat{B_1}+\widehat{B_3}=\dfrac{180^0}{2}\)

\(\Rightarrow\widehat{B_1}+\widehat{B_2}=90^0\)

Hay \(\widehat{FBD}=90^0\)

\(\Rightarrow BO\perp BF\)

b, Ta có:

\(\widehat{A_1}+\widehat{A_2}=\dfrac{1}{2}\widehat{BAC}\)

Hay: \(\widehat{A_1}+\widehat{A_2}=\dfrac{1}{2}120^0=60^0\)

Lại có: \(\widehat{A_3}+\widehat{BAC}=180^0\)( 2 góc kề bù)

Hay: \(\widehat{A_3}+120^0=180^0\)

\(\widehat{A_3}=180^0-120^0\)

\(\widehat{A_3}=60^0\)

Vẽ Ay là tia đối AD

\(\Rightarrow\widehat{A_1}=\widehat{A_4}\)

\(\Rightarrow\widehat{A_1}=\widehat{A_3}=\widehat{A_4}=60^0\)

\(\Rightarrow\) AF là tia phân giác \(\widehat{FAy}\) (\(\widehat{A_3}=\widehat{A_4}\))

Ta có: \(\widehat{B_3}=\widehat{B_4}\) ( BF là đường phân giác \(\widehat{xBA}\)) (gt)

Mà: F là giao điểm 2 tia phân giác AF; BE

\(\Rightarrow\) DF là tia phân giác \(\widehat{BDA}\)

\(\Rightarrow\widehat{BDF}=\widehat{ADF}\)

Answer 2

[Akabane Karma]

sao lại cắt các cạnh BC và AC lần lượt ở D và E