Nêu định lí về dấu của nhị thức bậc nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2018
- Nhị thức \(f\left(x\right)=a\)\(x+b\left(a\ne0\right)\) cùng dấu với hệ số \(a\) khi \(x\) lấy giá trị trong khoảng \(\left(\frac{-b}{a};+\infty\right)\) và trái dấu với hệ số \(a\) khi \(x\) lấy các giá trị trong khoảng \(\left(-\infty;\frac{-b}{a}\right)\).
24 tháng 6 2018
Nhị thức bậc nhất đối với x là biểu thức dạng f(x) = ax + b, trong đó a và b là hai số cho trước, với a ≠ 0 và a được gọi là hệ số của x hay hệ số của nhị thức. |
CM
10 tháng 1 2018
Định lí (trang 101 sgk Đại Số 10):
Cho tam thức f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac
- Nếu Δ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ R.
- Nếu Δ = 0 thì f(x) cùng dấu với hệ số a với mọi x ≠ -b/2a.
- Nếu Δ > 0 thì f(x) cùng dấu với hệ số a khi x < x1 hoặc x > x2
f(x) trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 là hai nghiệm của f(x) và x1 < x2.
6 tháng 4 2017
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2022
Do \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall x\) nên BPT tương đương:
\(-3\left(x^2+x+1\right)\le x^2-3x-1\le3\left(x^2+x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-1\ge-3x^2-3x-3\\x^2-3x-1\le3x^2+3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2\ge-2\left(luôn-đúng\right)\\2x^2+6x+4\ge0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
TT
0
CM
1 tháng 6 2017
Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).
KV
10 tháng 5 2023
a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c)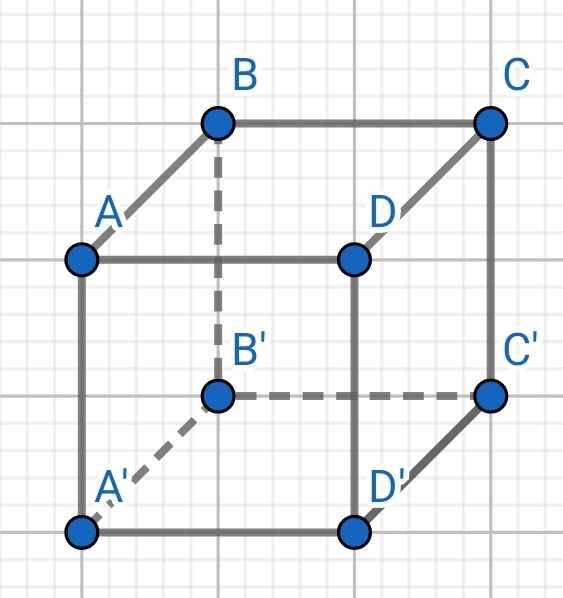 
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
10 tháng 5 2023
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3
nè: Nhị thức bậc nhất-Dấu của nhị thức bậc nhất - Công thức học tập