Cho ∆ABC vuông tại A ( AB < AC ), vẽ đường cao AH ( H thuộc BC )
a) Chứng minh : ∆ACH ~ ∆BCA, từ đó suy ra AH.BC = AB.AC
b) Gọi K, I lần lượt là trung điểm của HC và AH ( K thuộc HC, I thuộc AH ). Chứng minh : ∆HIK ~ ∆ABC
c) Vẽ HE, HF lần lượt vuông góc AB, AC ( E thuộc AB, F thuộc AC ). Chứng minh : AH3 = AE.AF.BC
d) Cho BA = 3cm, BC = 5cm. Tính độ dài AE




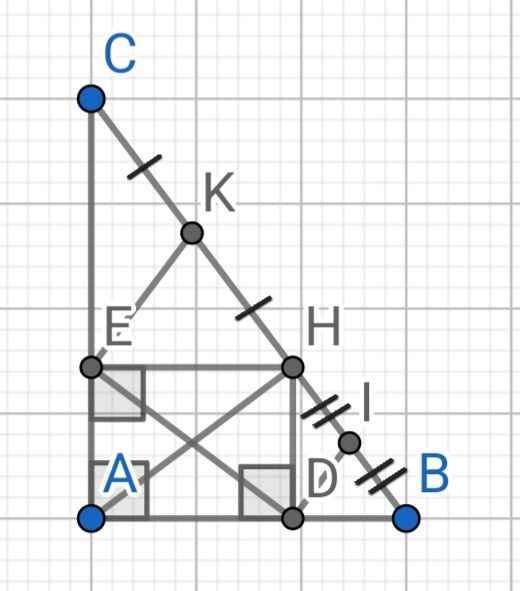
a: XétΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
Do đó: ΔACH\(\sim\)ΔBCA
Suy ra: AH/BA=AC/BC
hay \(AH\cdot BC=AB\cdot AC\)
b: Xét ΔHAC có
I là trung điểm của HA
K là trung điểm của HC
DO đó: IK là đường trung bình
=>IK//AC
=>ΔHIK\(\sim\)ΔHCA
mà ΔHCA\(\sim\)ΔACB
nên ΔHIK\(\sim\)ΔACB