Cho G là trọng tâm của tam giác đều ABC. CMR: GA=GB=GC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
21 tháng 9 2019
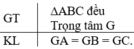
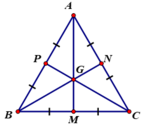
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
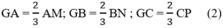
Từ (1) , (2) ⇒ GA = GB = GC.
US
1
7 tháng 4 2016
GA=GB=GC, G là trọng tâm tam giác kkhi và chỉ khi đso là tam giác đều.
Đề sai
CT
0
TT
0
BM
4
6 tháng 1 2016
vì G là trọng tâm của tam giác ABC ta có :
AG=2/3 AN
BG=2/3 BQ (1)
CG=2/3 CM (2)
mà 2 tam giác ACM=ABQ ( g-c-g)
suy ra CM=BQ (cạnh tương ứng) (3)
từ (2) và (3) suy ra BG=CG
>>>>>>.........''tớ chỉ pk lmf tới đây thui''.........<<<<<<<<<<
NN
1
1 tháng 4 2016
làm sao để c/m 3 cạnh đó bằng nhau??????????? mk cx ko bít bn giống mk hihi
4536476598769
OT
1
TH
2
24 tháng 9 2017
* cái này là công thức rồi bn o cần chứng minh đâu
công thức : cho tam giác ABC ; nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
13 tháng 10 2022
Gọi M trung điểm BC
G đối xứng D qua M
=> tứ giác BGCD là hình bình hành
=> GD=2.GM (Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AG = 2.GM ( \(\dfrac{AG}{GM}=\dfrac{2}{1},GA=\dfrac{2}{3}AM\) )
⇒ AG=GD
Mặt khác, G ϵ AD
⇒\(\overrightarrow{AG}=\overrightarrow{GD}\)
Ta có \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (Quy tắc hình bình hành)
Nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}\) = \(\overrightarrow{GD}+\overrightarrow{GA}\)
Mà \(\overrightarrow{AG}=\overrightarrow{GD}\) (cmt)
⇒\(\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{AG}-\overrightarrow{AG}=\overrightarrow{O}\)
8 tháng 7 2023
a: AD=BE=CF=8*căn 3/2=4*căn 3(cm)
CG=2/3*4*căn 3=8/3*căn 3(cm)
b: Vì ΔABC đều có G là trọng tâm
nên G là tâm đường tròn ngoại tiếp
=>GA=GB=GC
ta có hình vẽ
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA =
AM; GB = 
BN; GC = 
CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC