Bài 6.Cho tam giác ABC có trung tuyến AM đồng thời là đường phân giác.
Trên tia AM lấy điểm D sao cho MD = MA. Chứng minh:
a) AB = CD b) ∆ACD cân tại C
c) ∆ABC cân tại A
Bài 7.Cho góc xOy có tia phân giác Ot. Trên tia Ot lấy điểm C bất kì. Lấy A ∈ Ox, B
∈ Oy sao cho OA = OB. Gọi H là giao điểm của AB và Ot. Chứng minh:
a) CA = CB và CO là tia phân giác của ACB
b) OC vuông góc với AB tại trung điểm của AB
c) Biết AB = 6cm, OA = 5cm. Tính OH.
Bài 8.Cho tam giác DEF cân tại D. Gọi I là giao điểm của các tia phan giác EP và
FQ.
a) Biết EIF " = 1100. Tính số đo góc D.
b) Biết D% = 500. Tính số đo ba góc của tam giác IPF.
Bài 9.Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C
cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến
AB, AC, BC. Biết KI = 1cm, BK = 2cm, KC = 3cm.
a) Chứng minh: ∆BHI= ∆BKI
b) Chứng minh tam giác AHI vuông cân
c) Tính chu vi tam giác ABC.
Mọi ng làm đc bài thì cho em xin hình luôn ak




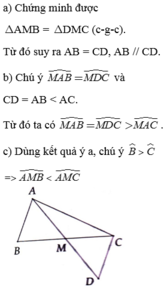

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
Suy ra: AB=DC
b: Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC
AM là đường phân giác ứng với cạnh BC
Do đó: ΔABC cân tại A
Suy ra: AB=AC
mà AB=CD
nên AC=CD
Xét ΔCAD có CA=CD
nên ΔCAD cân tại C