Diện tích tam giác ABM là
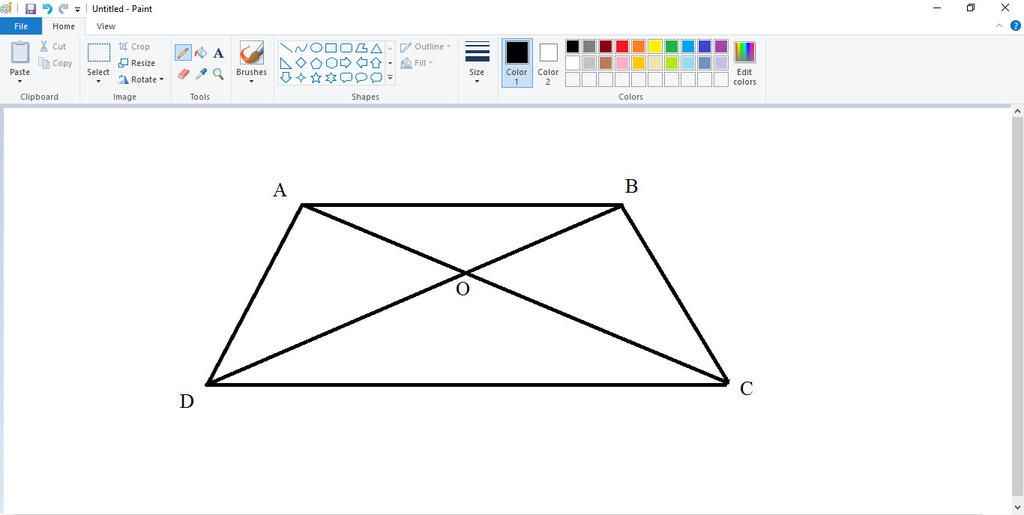
Gọi M, N theo thứ tự là trung điểm của BD và AC. Biết rằng OB = 2 MO, đáy lớn CD = 16 cm.
Vậy đáy nhỏ AB = cm. Câu 4:Kết quả phép tính
Trả lời:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bì này mink chữa nghỉ ra mink cũng đang tìm cách tính của nó
Theo đề ta có : EC= 1/2 ED => EC= 1/3 CD => ED=2/3 DC
BM= 2/5 BC => MC= 3/5 BC
a)
Diện tích tam giác ABM là :( AB x BM)/2 = (AB x BC x 2/5)/2 = (48 x 2/5)/2 = 9,6 cm2
b)
Diện tích tam giác CEM là : (CE x MC)/2 = (1/3 DC x 3/5 BC)/2 = (48 x 1/3 x 3/5 )/2 = 4,8 cm2
Tỉ số diện tích tam giác ABM và CEM là : 9,6:4,8 = 2:1
c)
Diện tích tam giác ADE là : (AD x DE)/2 = (AD x DC x 2/3)/2 = (48 x 2/3)/2 = 16 cm2
Diện tích tam giác AEM là : SABCD - SABM - SCEM - SADE = 48 - 9,6 - 4,8 - 16 = 17,6 cm2

bài 2
Cặp hình tam giác có diện tích bằng nhau là:
+ AOD và BOC
+ ADB và ABC
+ ADC và BCD
hình:

a: S ACB=24cm2
=>S AMB=2/5*24=9,6cm2
b: S BDC=24cm2
=>S BEC=8cm2
=>S EMC=4,8cm2
=>S ABM/S EMC=2

a) Diện tích tam giác ABM là :
72 . (1 - 3/4) = 18 (cm2)
Diện tích tam giác MNC là :
72. 1/4 = 18 (cm2)
=> ABM = MNC
b) Diện tích AMN là :
72 - (18 + 18) = 36 (cm2)

THAM KHẢO NHA!!!!! CÓ THỂ KHÔNG GIỐNG LẮM!!!!! LÀM TƯƠNG TỰ NHA!!!!!
Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC
Câu 1:
\(\frac{x+1}{2002}+\frac{x+2}{2001}+\frac{x+3}{2000}=\frac{x+4}{1999}+\frac{x+5}{1998}+\frac{x+6}{1997}\)
\(\Rightarrow\left(1+\frac{x+1}{2002}\right)+\left(1+\frac{x+2}{2001}\right)+\left(1+\frac{x+3}{2000}\right)=\left(1+\frac{x+4}{1999}\right)+\left(1+\frac{x+5}{1998}\right)+\left(1+\frac{x+6}{1997}\right)\)
\(\Rightarrow\frac{x+2003}{2002}+\frac{x+2003}{2001}+\frac{x+2003}{2000}=\frac{x+2003}{1999}+\frac{x+2003}{1998}+\frac{x+2003}{1997}\)
\(\Rightarrow\frac{x+2003}{2002}+\frac{x+2003}{2001}+\frac{x+2003}{2000}-\frac{x+2003}{1999}-\frac{x+2003}{1998}-\frac{x+2003}{1997}=0\)
\(\Rightarrow\left(x+2003\right)\left(\frac{1}{2002}+\frac{1}{2001}+\frac{1}{2000}-\frac{1}{1999}-\frac{1}{1998}-\frac{1}{1997}\right)=0\)
Mà \(\frac{1}{2002}+\frac{1}{2001}+\frac{1}{2000}-\frac{1}{1999}-\frac{1}{1998}-\frac{1}{1997}\ne0\)
\(\Rightarrow x+2003=0\)
\(\Rightarrow x=-2003\)
Vậy x = -2003
Câu 6:
Giải:
Áp dụng định lí Py-ta-go vào \(\Delta ABC\left(\widehat{B}=90^o\right)\) có:
\(\Rightarrow AB^2+BC^2=AC^2\)
\(\Rightarrow6^2+BC^2=10^2\)
\(\Rightarrow BC^2=64\)
\(\Rightarrow BC=8\)
\(\Rightarrow S_{ABCD}=8.6=48\left(cm^2\right)\)
Vậy...