trong mặt phẳng oxyz cho tứ diện ABCD có A(2;3;1),B(4;1;-20,c(6;3;7),D(-5;-4;-8).độ dài đường cao kẻ từ d cảu tứ diện là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 3 2017
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
Từ đó ta có:
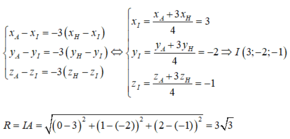
Vậy đáp án C đúng.
CM
7 tháng 3 2017
Đáp án B
* Tam giác ABC có MN là đường trung bình nên MN // BC (1)
Tam giác ACD có NP là đường trung bình nên NP // CD (2)
Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).
* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là i → (1; 0; 0) nên mặt phẳng (MNP) có VTPT i → (1; 0; 0).
* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).
* Phương trình mặt phẳng (MNP) là:
1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0
Chọn B.
CM
6 tháng 11 2017
Đáp án D.
Ta có:
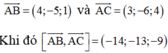
Phương trình mặt phẳng (ABC) là:
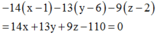
Do đó
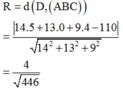
Vậy phương trình mặt cầu tâm D tiếp xúc với mặt phẳng (ABC) là:
CM
15 tháng 12 2019
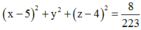
Chọn D.
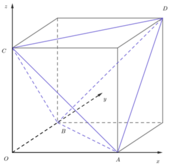
Phương pháp: Tứ diện ABCD có các cặp cạnh đối diện bằng nhau là tứ diện gần đều.
Cách giải: Theo giả thiết suy ra:
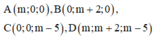
Theo tính chất của tứ diện gần đều tâm mặt cầu ngoại tiếp I của tứ diện ABCD là trung điểm OD
CM
25 tháng 11 2018
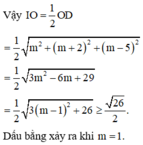
Chọn D
Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là:
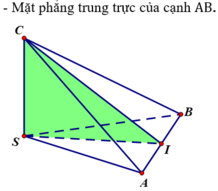
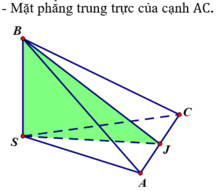
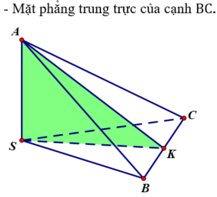
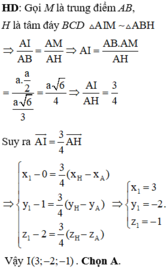
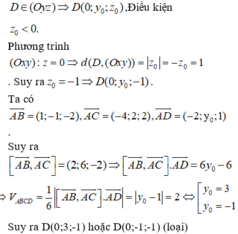
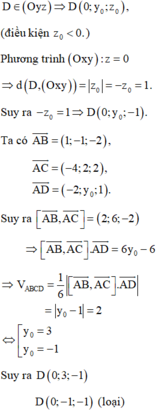
Lời giải:
Ta có \(\left\{\begin{matrix} \overrightarrow{AB}=(2,-2,-3)\\ \overrightarrow{AC}=(4,0,6)\end{matrix}\right.\Rightarrow \overrightarrow{n_{ABC}}=[\overrightarrow{AB},\overrightarrow{AC}]=4(-3,-6,2)\)
Suy ra PTMP \((ABC): 3x+6y-2z-22=0\)
Độ dài đường cao kẻ từ $D$ của tứ diện là:
\(d=\frac{|3.(-5)+6(-4)-2(-8)-22|}{\sqrt{3^2+6^2+2^2}}=\frac{45}{7}\)