Cho bảng ô vuông 8 * 8: Người ta điền vào mỗi ô vuông của bảng một số 1; 0 hoặc 1: Sau đó, người ta tính tổng của tất cả các số được điền ở các hàng, các côt và các đường chéo. Hỏi, các tổng
này có thể phân biệt nhau được không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Cách giải:

Nhận xét: Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì số lượng số 1 và số lượng số -1 trong mỗi hàng và mỗi cột đều là 2.
⇔ Mỗi hàng và mỗi cột đều có đúng 2 số 1.
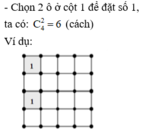
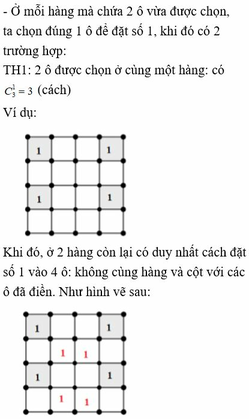
- Ở mỗi hàng mà chứa 2 ô vừa được chọn, ta chọn đúng 1 ô để đặt số 1, khi đó có 2 trường hợp:
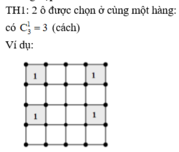
Khi đó, ở 2 hàng còn lại có duy nhất cách đặt số 1 vào 4 ô : không cùng hàng và cột với các ô đã điền. Như hình vẽ sau:
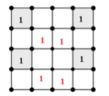
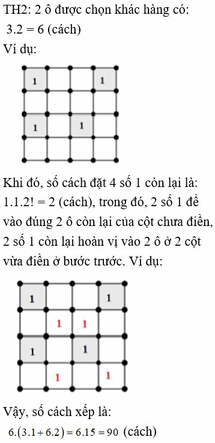
TH2: 2 ô được chọn khác hàng: có: 3.2 = 6 (cách)
Ví dụ:

Khi đó, số cách đặt 4 số 1 còn lại là: 1.1.2! = 2 (cách), trong đó, 2 số 1 để vào đúng 2 ô còn lại của cột chưa điền, 2 số 1 còn lại hoàn vị vào 2 ô ở 2 cột vừa điền ở bước trước. Ví dụ:


Trên mỗi hàng, mỗi cột phải có hai số -1, hai số 1.
Ta sẽ xếp theo hàng.
Ta có các khả năng của các hàng như sau:
(1) 1, 1, -1, -1
(2) 1, -1, -1, 1
(3) -1, -1, 1, 1
(4) -1, 1, -1, 1
(5) 1, -1, 1, -1
(6) -1, 1, 1, -1
Giả sử hàng 1 ta điền bộ (1). Ta có các trường hợp sau:
TH1: Hàng 2 điền bộ (1), khi đó hàng 3, hàng 4 ta phải điền bộ (3).
TH2: Hàng 2 điền bộ để tổng 2 số trong của các cột bằng 0, khi đó ta điền bộ (3). Hàng 3 và hàng 4 khi đó cũng phải điền sao cho tổng các cột trong hai hàng bằng 0. Có 6 cách điền như vậy.
TH3: Hàng 2 điền sao cho có 2 cột trong 4 cột có tổng bằng 0. Có 4 cách. Khi đó điền hàng 3 có 2 cách, điền hàng 4 có 1 cách. Tổng số cách là: 1.4.2.1=8 (cách).
Vậy có tổng số cách là: 6.(1 + 6 + 8) = 90 (cách).

Chọn B
Ta có ![]()
Xét A ¯ : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó ![]()
Vậy ![]()

Chọn đáp án C.
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
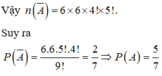


Vì ta có 8 hàng , 8 cột và hai đường chéo nên ta có 18 tổng phân biệt
trong khi tổng của 1 cột là nhơ hơn hoặc bằng 8
nên mỗi tổng chỉ có thể có 9 khả năng là \(0->8\)
theo nguyên lí dircihlet ta có tồn tại ít nhất một số từ 0 đến 8 sao cho nó là giá trị của ít nhất 2 cột
vậy các tổng không thể phân biệt nhau được