Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
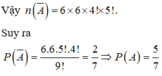

Đặt vào rồi nói nó có thể :) hí hí! !
Từ 1 => 16 có 8 cặp 1 + 16 .... 8+ 9 đều bằng nhau vậy thì mỗi cột chỉ cần 2 cặp như thế thì tất cả các cột có tổng là bằng nhau :)

a﴿ Chu vi:
2/5 x 4 = 8/5 ﴾m﴿
Diện tích:
2/5 x 2/5 = 4/25 ﴾m2 ﴿
b﴿ Diện tích 1 ô vuông nhỏ là:
2/25 x 2/25 = 4/625 ﴾m2 ﴿
Số ô vuông cắt được là:
4/25 : 4/625 = 25 ﴾ô vuông﴿
c﴿ Chiều rộng tờ giấy hình chữ nhật là:
4/25 : 4/5 = 1/5 ﴾m﴿

\(1\frac{1}{3}=\frac{4}{3}\)
Phân số chỉ số hàng đã chuyển đi so với số hàng trong kho là :
\(\frac{3}{7}\cdot\frac{4}{3}=\frac{4}{7}\)(số hàng trong kho lúc đầu)
Phân số chỉ số hàng tăng lên là :
\(\frac{4}{7}-\frac{3}{7}=\frac{1}{7}\)(số hàng trong kho lúc đầu)
Số hàng trong kho lúc đầu là :
\(101:\frac{1}{7}=707\)(tấn)

Chọn B.
Cách giải:
Nhận xét: Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì số lượng số 1 và số lượng số -1 trong mỗi hàng và mỗi cột đều là 2.
⇔ Mỗi hàng và mỗi cột đều có đúng 2 số 1.
- Ở mỗi hàng mà chứa 2 ô vừa được chọn, ta chọn đúng 1 ô để đặt số 1, khi đó có 2 trường hợp:
Khi đó, ở 2 hàng còn lại có duy nhất cách đặt số 1 vào 4 ô : không cùng hàng và cột với các ô đã điền. Như hình vẽ sau:
TH2: 2 ô được chọn khác hàng: có: 3.2 = 6 (cách)
Ví dụ:
Khi đó, số cách đặt 4 số 1 còn lại là: 1.1.2! = 2 (cách), trong đó, 2 số 1 để vào đúng 2 ô còn lại của cột chưa điền, 2 số 1 còn lại hoàn vị vào 2 ô ở 2 cột vừa điền ở bước trước. Ví dụ: