K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)
3 tháng 1 2021
Ta có: \(\left(x-1\right)^{2020}\ge0\forall x\)
\(\left|y-3\right|\ge0\forall y\)
Do đó: \(\left(x-1\right)^{2020}+\left|y-3\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\y-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Vậy: (x,y)=(1;3)
27 tháng 12 2017
M N P Q X Y
Kẻ ba đường cao của ΔYMN , ΔXPQ và tứ giác MNPQ
=> Ba đường cao này bằng nhau vì cùng vuông góc với hai đường thẳng MN , PQ song song với nhau
Gọi h là độ dài ba đường cao
Ta có :
\(S_{YMN}=\dfrac{PQ.h}{2}\)
\(S_{XPQ}=\dfrac{MN.h}{2}\)
\(\Rightarrow S_{YMN}+S_{XPQ}=\dfrac{PQ.h}{2}+\dfrac{MN.h}{2}=\dfrac{PQ.h+MN.h}{2}=\dfrac{\left(PQ+MN\right).h}{2}=S_{MNPQ}\left(đpcm\right)\)
6 tháng 11 2021
Vì MNQP là hcn nên \(MQ=NP=4\left(cm\right);QP=\sqrt{MQ^2+MN^2}=\sqrt{65}\left(cm\right)\left(pytago\right)\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 3 2023
Xét \(\Delta MQN\) và \(\Delta PNQ\) có:
\(\widehat{NQP}=\widehat{MNQ}\) (Vì \(MN//PQ\) nên đó là hai góc so le trong)
\(\widehat{MQN}=\widehat{QNP}\) ( Vì \(MQ//NP\) nên hai góc đó là góc so le trong)
\(QN\) là cạnh chung
\(\Rightarrow\Delta MQN=\Delta PNQ\left(g-c-g\right)\)
a) Do △MQN=△PNQ nên
\(\Rightarrow MN=PQ\) (2 cạnh tương ứng)
b) Do △MQN=△PNQ nên
\(\Rightarrow MQ=NP\) (2 cạnh tương ứng)
ZR
5
24 tháng 8 2021
\(\dfrac{x}{4}=\dfrac{y}{3}\) áp dụng...ta đc:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{21}{7}=3\)
x:4=3
x=12
y:3=3
y=9
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Vì \(\widehat {MNQ} = \widehat {PQN}( = 35^\circ )\), mà hai góc này ở vị trí so le trong nên MN // QP. (Dấu hiệu nhận biết hai đường thẳng song song)
28 tháng 10 2023
vì góc MNQ và NQP là e góc solo trong bằng nhau
su ra MN//QP
PN
0
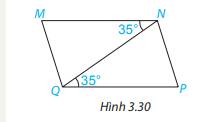
x=70
y=50
Gọi \(\widehat{M_1}=50^o;\widehat{P_1}=70^o\)
\(\Rightarrow\hept{\begin{cases}\widehat{M_1}+\widehat{NMQ}=180^o\\\widehat{P_1}+\widehat{QPN}=180^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{NMQ}=180^o-50^o=130^o\\\widehat{QPN}=180^o-70^o=110^o\end{cases}}\)
\(MN//QP\Rightarrow\hept{\begin{cases}\widehat{NMQ}+\widehat{MNP}=180^o\\\widehat{MQP}+\widehat{QPN}=180^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{MNP}=180^o-130^o=50^o\Leftrightarrow y=50^o\\\widehat{MQP}=180^o-110^o=70^o\Leftrightarrow x=70^o\end{cases}}\)