TAM GIÁC ABC CÓ AB=12, BC=18, CA=27. TAM GIÁC A'B'C' CÓ A'B'=12, B'C'=18, C'A;=8. HAI TAM GIÁC CÓ ĐỒNG DẠNG KO? CM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
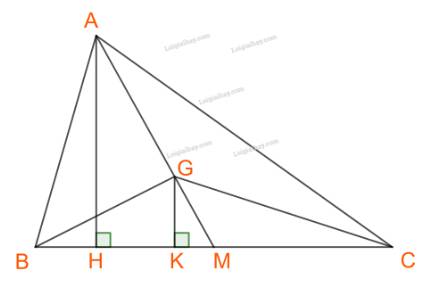
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)



Đổi 3dm =30cm
Chu vi hình tam giá ABC là
[ 27 + 33+ 30 ] :3 =30 dm
Ta có: AB+BC=27 cm
BC+CA=33 cm
CA+AB=3 dm = 30 cm
suy ra: AB+BC+BC+CA+CA+AB=27+33+30=90 cm
2 x ( AB + BC + CA ) = 90 cm
AB + BC + CA = 90 : 2 = 45 cm
Vậy chu vi tam giác ABC là 45 cm

3dm=30cm vì AB ,BC,CA được tính 2 lần nên:
2 lần chu vi tam giác là:
27+33+30=90(cm)
Chu vi tam giác là:
90:2=45(cm)
Đ/S45cm
Xét \(\Delta ABC \ và \ \Delta C'B'A'\)có:
\(\dfrac{AB}{C'A'}=\dfrac{12}{8}=\dfrac{3}{2}\\ \dfrac{BC}{A'B'}=\dfrac{18}{12}=\dfrac{3}{2}\\ \dfrac{CA}{B'C'}=\dfrac{27}{18}=\dfrac{3}{2}\\ =>\dfrac{AB}{C'A'}=\dfrac{BC}{A'B'}=\dfrac{CA}{B'C'}\)
=>\(\Delta ABC\) đồng dạng vs \(\Delta C'B'A'\)