Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo đề bài ta có:
\(\overline{X}\)=(10.25+42.9+8.x+7.15+6.y):100=8,69
=>250+378+105+8x+6y =869
=>733+8x+6y =869
=> 8x+6y =136 (*)
Ta có: 25+42+x+15+y=100
82+x+y =100
x+y =18 (**)
* Ta có: x+y=18
=>6x+6y =108
Kết hợp (*) và (**), ta có:
8x+6y-(6x+6y)=136-108
8x+6y-6x-6y=28
2x =28
x =14
=>y=18-14=4
Gọi số lần bắn được 8 là x
Số lần bắn được 6 là y (x,y\(\in\)N* )
Tổng số lần bắn là 100 . Ta có PT
25+42+x+15+y=100
\(\Leftrightarrow\)x+y=18 (1)
Điểm số trung bình là 8,69 nên ta có PT:
\(\dfrac{10.25+9.42+8x+7.15+6y}{100}=8,69\)
\(\Leftrightarrow\)4x+3y=68(2)
Từ (1) , (2) ta có hệ \(\left\{{}\begin{matrix}x+y=18\\4x+3y-68\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=14\\y=4\end{matrix}\right.\)tmđk
Vậy số lần bắn được điểm 8 là 14 lần
Số lần bắn được điểm 6 là 4 lần
Gọi số lần bắn đạt điểm 8 là x, số lần bắn đạt điểm 6 là y.
Điều kiện x, y ∈ N; x < 18, y < 18.
Tổng số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 ⇔ x + y = 18.
Điểm trung bình là :
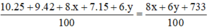
Điểm trung bình bằng 8,69 nên ta có phương trình :
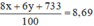⇔ 8x + 6y + 733 = 869 ⇔ 8x + 6y = 136
Ta có hệ phương trình :
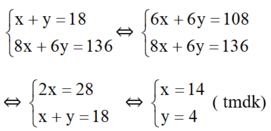
Vậy số lần bắn đạt 8 điểm là 14 và số lần bắn đạt 6 điểm là 4.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Gọi số lần bắn đạt điểm 8 là x, số lần bắn đạt điểm 6 là y.
Điều kiện x, y ∈ N; x < 18, y < 18.
Tổng số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 ⇔ x + y = 18.
Điểm trung bình là :
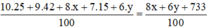
Điểm trung bình bằng 8,69 nên ta có phương trình :
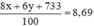⇔ 8x + 6y + 733 = 869 ⇔ 8x + 6y = 136
Ta có hệ phương trình :
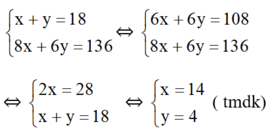
Vậy số lần bắn đạt 8 điểm là 14 và số lần bắn đạt 6 điểm là 4.
Số điểm bị trừ của vận động viên A là : 2 x 3 = 6 ( điểm )
Tổng số điểm của vận động viên A là :( 2 x 8) + (3 x 9) + (3 x 10) - 6 = 67 ( điểm )
Vậy tổng số điểm của vận động viên A là 67 điểm
Chúc bạn học tốt
Vân động viên A bắn được số điểm là: 8*2+9*3+3*10-2*3=67 điểm
Vậy vận động viên A bắn được 67 điểm
Ta thấy : Nếu bắn 13 viên thì tổng số điểm ít nhất là : 13 x 8 = 104 (điểm)
Vậy vận động viên đó đã bắn12 viên.
Nếu tất cả đều trúng vòng 8 thì số điểm đạt được là : 12 x 8 = 96 (điểm)
So với 100 điểm thì còn thiếu : 100 - 96 = 4 (điểm)
Như vậy phải thay 1 số viên vòng 8 bằng vòng 9 và vòng 10.
1 viên vòng 9 so với 1 viên vòng 8 thì tăng thêm 1 điểm còn 1 viên vòng 10 so với 1 viên vòng 8 thì tăng thêm 2 điểm.
Ta có : 4 = 1 + 1 + 1 + 1 = 1 + 1 + 2 = 2 + 2
Vì tất cả các vòng đều có viên trúng nên phải thay 1 viên vòng 8 bằng 1 viên vòng 10 và 2 viên vòng 8 bằng 2 viên vòng 9
Vậy người đó đã bắn 12 viên trong đó có 9 viên trúng vòng 8, có 2 viên trúng vòng 9 và 1 viên trúng vòng 10.
=))
Một cách giải khác cho các bạn học THCS:
Gọi số viên các vòng 8 điểm , 9 điểm , 10 điểm lần lượt là a, b, c ( a, b, c >0 , thi=uộc N)
=> a +b + c \(\ge\) 12 (1)
và 8a + 9b +10 c = 100
Giả sử a + b + c \(\ge\)13
=> \(8a+8b+8c\ge104>100=8a+9b+10c\) vô lí
=> a + b+ c < 13 (2)
Từ (1) ; (2) => a +b +c =12
=> a = 12 -b -c
Thế vào 8a +9b +10 c = 100
Có: 8 ( 12 -b - c ) + 9b +10 c =100
=> b + 2c = 4
=> b = 2 và c = 1=> a =9
=> kết luận như bạn làm bên dưới.
Ít nhất mỗi vòng trúng 2 viên với số điểm tương ứng là: 8x2+9x2+10x2 =54, 5 viên còn lại đạt: 103-54 =49 nên 4 viên bắn vào vòng 10 điểm , 1 viên vòng 9 điểm. Vậy 2 vòng 8, 3 vòng 9, 6 vòng 10
Ít nhất mỗi vòng trúng 2 viên với số điểm tương ứng là: 8x2+9x2+10x2 =54, 5 viên còn lại đạt: 103-54 =49 nên 4 viên bắn vào vòng 10 điểm , 1 viên vòng 9 điểm. Vậy 2 vòng 8, 3 vòng 9, 6 vòng 10
