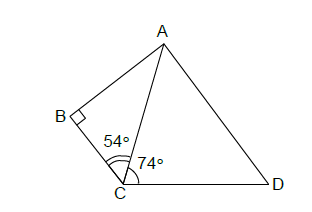
Trong hình bên, AC = 8cm AD = 9,6cm ABC = 90° ACB = 54° và ACD = 74°. Hãy tính:
a) AB
b) ACD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A B = A C . sin C = 8 . sin 54 ° = 6 , 47 ( c m )
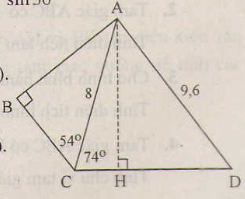
b) Trong tam giác ACD, kẻ đường cao AH.
Ta có: A H = A C . sin A C H = 8 . sin 74 ° 7 , 69 ( c m )
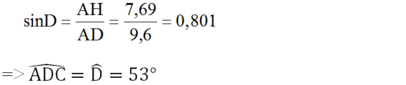


a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Trong tam giác ACD, kẻ đường cao AH.
Ta có: AH = AC . sinACH = 8.sin74o 7,69 (cm)
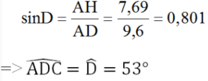

Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)

| Gt | \(\Delta ABC\), \(\Delta ADC\) AB = AD \(\widehat{ABC}\) = \(\widehat{ADC}\) = 90o |
| Kl | \(\widehat{ACD}\) = \(\widehat{ACB}\) |
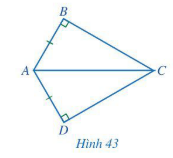
Vì ΔABC có \(\widehat{ABC}\)=90o (gt) nên ∆ABC vuông tại B.
Vì ∆ADC có \(\widehat{ADC}\)=90° (gt) nên ∆ADC vuông tại D.
Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:
AC là cạnh chung
AB = AD (gt)
Suy ra Δ∆ABC = ∆ADC (cạnh huyền – cạnh góc vuông)
Do đó \(\widehat{ACB}\)=\(\widehat{ADC}\) (hai góc tương ứng)
Vậy \(\widehat{ACB}=\widehat{ACD}\)

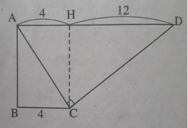
Kẻ đường cao CH của tam giác ACD vuông tại C. Khi đó
AH = BC = 4, HD = AD – AH = 12.
Từ đó
H C 2 = HA.HD = 48, vậy HC = 4 3
Trong tam giác vuông HCD, ta có
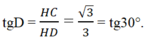
Nên ∠ D = 30 ° . Suy ra ∠(BCD) = 180 ° - 30 ° = 150 °